Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T21:40:39.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean-square stability of a class of stochastic integral equations

Published online by Cambridge University Press:  17 April 2009

W.J. Padgett
W.J. Padgett
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, South Carolina, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The object of this paper is to investigate under very general conditions the existence and mean-square stability of a random solution of a class of stochastic integral equations in the form

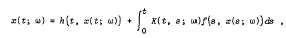
for t ≥ 0, where a random solution is a second order stochastic process {x(t; w) t ≥ 0} which satisfies the equation almost certainly. A random solution x(t; w) is defined to be stable in mean-square if E[|x(t; w)|2] ≤ p for all t ≥ 0 and some p > 0 or exponentially stable in mean-square if E[|x(t; w)|2] ≤ pe-at, t ≥ 0, for some constants ρ > 0 and α > 0.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 7 , Issue 3 , December 1972 , pp. 337 - 352
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Bharucha-Reld, A.T., “On the theory of random equations”, Proc. Sympos. Appl. Math. 16, 40–69 (American Mathematical Society, Providence, Rhode Island, 1964).Google Scholar
[2]Bharucha-Reid, A.T., Random integral equations (Academic Press, New York, to be published).Google Scholar
[3]Boyd, D.W. and Wong, J.S.W., “On nonlinear contractions”, Proc. Amer. Math. Soc. 20 (1969), 458–464.CrossRefGoogle Scholar
[4]Corduneanu, C., “Problèmes globaux danss le théorie des équations intégrales de Volterra”, Ann. Mat. Pura Appl. 67 (1965), 349–363.CrossRefGoogle Scholar
[5]Fortet, Robert M., “Random distributions with an application to telephone engineering”, Proc. Third Berkeley Sympos. Math. Statist. Probability, 2 (1954–1955), 81–88 (University of California Press, Berkeley, Los Angeles, 1956).Google Scholar
[6]Kelley, J.L., General topology (Van Nostrand, Toronto, New York, London, 1955).Google Scholar
[7]Loève, Michel, Probability theory, 3rd ed. (Van Hostrand, Princeton, New Jersey; Toronto, Ontario; London; 1963).Google Scholar
[8]Milton, J. Susan, Padgett, W.J. and Tsokos, Chris P., “On the existence and uniqueness of a random solution to a perturbed random integral equation of the Fredholm type”, SIAM J. Appl. Math. 22 (1972), 194–208.CrossRefGoogle Scholar
[9]Morozan, T., “Stability of linear systems with random parameters”, J. Differential Equations 3 (1967), 170–178.CrossRefGoogle Scholar
[10]Hashed, M.Z. and Wong, J.S.W., “Some variants of a fixed point theorem of Krasnoselskii and applications to nonlinear integral equations”, J. Math. Meah. 18 (1969), 767–777.Google Scholar
[11]Padgett, W.J. and Tsokos, C.P., “On a semi-stochastic model arising in a biological system”, Math. Biosci. 9 (1970), 105–117.CrossRefGoogle Scholar
[12]Padgett, W.J. and Tsokos, C.P., “A stochastic model of chemotheraphy: Computer similation”, Math. Biosci. 9 (1970), 119–133.CrossRefGoogle Scholar
[13]Padgert, W.J. and Tsokos, C.P., “On a stochastic integral equation of the Volterra type in telephone traffic theory”, J. Appl. Probability 8 (1971), 269–275.CrossRefGoogle Scholar
[14]Padgett, W.J. and Tsokos, C.P., “Existence of a solution of a stochastic integral equation in turbulence theory”, J. Math. Phys. 12 (1971), 210–212.CrossRefGoogle Scholar
[15]Tsokos, C.P., “On some stochastic differential systems”, Proc. Third Annual Princeton Conf. on Inf. Sciences and Systems, 1969, 228–234.Google Scholar
[16]Tsokos, Chris P., “On the classical stability theorem of Poincaré-Lyapunov with a random parameter”, Proc. Japan Acad. 45 (1969), 781–785.Google Scholar
[17]Tsokos, Chris P., “On a stochastic integral equation of the Volterra type”, Math. Systems Theory 3 (1969), 222–231.CrossRefGoogle Scholar
[18]Tsokos, C.P. and Hamdan, M.A., “Stochastic nonlinear integro-differential systems with time-lag”, J. Natur. Sci. and Math. 10 (1970), 293–303.Google Scholar
[19]Tsokos, Chris P. and Hamdan, M.A., “Stochastic asymptotic exponential stability of stochastic integral equations”, J. Appl. Probability 9 (1972), 169–177.CrossRefGoogle Scholar