Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T02:31:08.882Z Has data issue: false hasContentIssue false
  • English
  • Français

MAXIMUM CUTS IN GRAPHS WITHOUT WHEELS

Part of: Graph theory

Published online by Cambridge University Press:  26 December 2018

JING LIN Open the ORCID record for JING LIN [Opens in a new window] ,
QINGHOU ZENG Open the ORCID record for QINGHOU ZENG [Opens in a new window]  and
FUYUAN CHEN
JING LIN
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian 350003, China College of Mathematics and Physics, Fujian University of Technology, Fujian 350118, China email [email protected]
QINGHOU ZENG*
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, China email [email protected]
FUYUAN CHEN
Affiliation:
Institute of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, Anhui 233030, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a graph 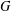$G$, let 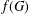$f(G)$ denote the maximum number of edges in a bipartite subgraph of 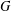$G$. Given a fixed graph 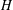$H$ and a positive integer 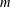$m$, let 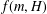$f(m,H)$ denote the minimum possible cardinality of 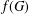$f(G)$, as 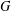$G$ ranges over all graphs on 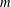$m$ edges that contain no copy of 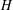$H$. Alon et al. [‘Maximum cuts and judicious partitions in graphs without short cycles’, J. Combin. Theory Ser. B 88 (2003), 329–346] conjectured that, for any fixed graph 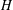$H$, there exists an 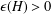$\unicode[STIX]{x1D716}(H)>0$ such that 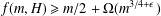$f(m,H)\geq m/2+\unicode[STIX]{x1D6FA}(m^{3/4+\unicode[STIX]{x1D716}})$. We show that, for any wheel graph 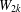$W_{2k}$ of 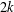$2k$ spokes, there exists 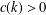$c(k)>0$ such that 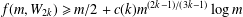$f(m,W_{2k})\geq m/2+c(k)m^{(2k-1)/(3k-1)}\log m$. In particular, we confirm the conjecture asymptotically for 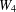$W_{4}$ and give general lower bounds for 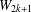$W_{2k+1}$.

Keywords

maximum cutH-freewheel graph

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C70: Factorization, matching, partitioning, covering and packing
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 13 - 26
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The research of the first author is supported by Youth Foundation of Fujian Province (Grant No. JAT170398) and Foundation of Fujian University of Technology (Grant No. GY-Z15086); the research of the second author is supported by the Postdoctoral Science Foundation of China (Grant No. 2018M632528) and the Fundamental Research Funds for the Central Universities (Grant No. WK0010460005); the research of the third author is supported by NSFC (Grant No. 11601001).

References

Alon, N., ‘Bipartite subgraphs’, Combinatorica 16 (1996), 301–311.Google Scholar
Alon, N., Bollobás, B., Krivelevich, M. and Sudakov, B., ‘Maximum cuts and judicious partitions in graphs without short cycles’, J. Combin. Theory Ser. B 88 (2003), 329–346.Google Scholar
Alon, N. and Halperin, E., ‘Bipartite subgraphs of integer weighted graphs’, Discrete Math. 181 (1998), 19–29.Google Scholar
Alon, N., Krivelevich, M. and Sudakov, B., ‘Maxcut in H-free graphs’, Combin. Probab. Comput. 14 (2005), 629–647.Google Scholar
Bollobás, B. and Scott, A. D., ‘Better bounds for Max Cut’, in: Contemporary Combinatorics, Bolyai Society Mathematical Studies, 10 (Springer, Berlin, 2002), 185–246.Google Scholar
Bollobás, B. and Scott, A. D., ‘Problems and results on judicious partitions’, Random Structures Algorithms 21 (2002), 414–430.Google Scholar
Edwards, C. S., ‘An improved lower bound for the number of edges in a largest bipartite subgraph’, in: Recent Advances in Graph Theory: Proc. 2nd Czechoslovak Sympos. Graph Theory, Academia, Praha (1975), 167–181.Google Scholar
Erdős, P., ‘Problems and results in graph theory and combinatorial analysis’, in: Graph Theory and Related Topics: Proc. Conf. Waterloo, 1977 (Academic Press, New York, 1979), 153–163.Google Scholar
Erdős, P. and Gallai, T., ‘Maximal paths and circuits in graphs’, Acta Math. Acad. Sci. Hungar. 10 (1959), 337–356.Google Scholar
Erdős, P., Gyárfás, A. and Kohayakawa, Y., ‘The size of the largest bipartite subgraphs’, Discrete Math. 177 (1997), 267–271.Google Scholar
Jensen, T. R. and Toft, B., Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization (John Wiley, New York, 1995).Google Scholar
Kostochka, A., Sudakov, B. and Verstraëte, J., ‘Cycles in triangle-free graphs of large chromatic number’, Combinatorica 37 (2017), 481–494.Google Scholar
Li, Y., Rousseau, C. and Zang, W., ‘Asymptotic upper bounds for Ramsey functions’, Graphs Combin. 17 (2001), 123–128.Google Scholar
Locke, S. C., ‘Maximum k-colorable subgraphs’, J. Graph Theory 6 (1982), 123–132.Google Scholar
Pikhurko, O., ‘A note on the Turán function of even cycles’, Proc. Amer. Math. Soc. 140 (2012), 3687–3692.Google Scholar
Poljak, S. and Tuza, Zs., ‘Bipartite subgraphs of triangle-free graphs’, SIAM J. Discrete Math. 7 (1994), 307–313.Google Scholar
Scott, A. D., ‘Judicious partitions and related problems’, in: Surveys in Combinatorics, London Mathematical Society Lecture Note Series, 327 (Cambridge University Press, Cambridge, 2005), 95–117.Google Scholar
Shearer, J., ‘A note on bipartite subgraphs of triangle-free graphs’, Random Structures Algorithms 3 (1992), 223–226.Google Scholar
Wei, V. K., ‘A lower bound on the stability number of a simple graph’, in: Bell Laboratories Technical Memorandum 81-11217-9 (Murray Hill, New Jersey, 1981).Google Scholar
Zeng, Q. and Hou, J., ‘Bipartite subgraphs of H-free graphs’, Bull. Aust. Math. Soc. 96 (2017), 1–13.Google Scholar
Zeng, Q. and Hou, J., ‘Maximum cuts of graphs with forbidden cycles’, Ars Math. Contemp. 15 (2018), 147–160.Google Scholar