No CrossRef data available.
Article contents
Maximum average distance in complex finite dimensional normed spaces
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A number r > 0 is called a rendezvous number for a metric space (M, d) if for any n ∈ ℕ and any x1,…xn ∈ M, there exists x ∈ M such that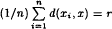 
. A rendezvous number for a normed space X is a rendezvous number for its unit sphere. A surprising theorem due to O. Gross states that every finite dimensional normed space has one and only one average number, denoted by r (X). In a recent paper, A. Hinrichs solves a conjecture raised by R. Wolf. He proves that 
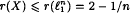for any n-dimensional real normed space. In this paper, we prove the analogous inequality in the complex case for n ≥ 3.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2002
References
[1]Baronti, M., Casini, E. and Papini, P. L., ‘On the average distance property and the size of the unit sphere’, Atti Sem. Mat. Fis. Univ. Modena, 46 (1998), 427–446.Google Scholar
[2]Cleary, J., Morris, S. A. and Yost, D., ‘Numerical geometry-numbers for shapes’, Amer. Math. Monthly 93 (1986), 260–275.Google Scholar
[3]García-Vázquez, J.C. and Villa, R., ‘The average distance property of the spaces 
and ’, Arch. Math. 76 (2001), 222–230.CrossRefGoogle Scholar
and 
’, Arch. Math. 76 (2001), 222–230.CrossRefGoogle Scholar[4]Gross, O., ‘The rendezvous value of a metric space’, Ann. of Math. Stud. 52 (1964), 49–53.Google Scholar
[5]Hinrichs, A., ‘The average distance property of classical Banach spaces’, Bull. Austral. Math. Soc. 62 (2000), 119–134.CrossRefGoogle Scholar
[6]Hinrichs, A., ‘Averaging distances in finite dimensional normed spaces and John's ellipsoid’, Proc. Amer. Math. Soc. 130 (2001), 579–584.CrossRefGoogle Scholar
[7]Lin, P-K., ‘The average distance property of Banach spaces’, Arch. Math. 68 (1997), 496–502.Google Scholar
[8]Morris, S.A. and Nickolas, P., ‘On the average distance property of compact connected metric spaces’, Arch. Math. 40 (1983), 459–463.Google Scholar
[9]Nickolas, P. and Yost, D., ‘The average distance property for subsets of Euclidean space’, Arch. Math. 50 (1988), 380–384.Google Scholar
[10]Stadje, W., ‘A property of compact connected spaces’, Arch. Math. 36 (1981), 275–280.CrossRefGoogle Scholar
[11]Tomczak-Jaegermann, N., Banach-Mazur distances and finite dimensional operator ideals, Pitman Monographs and Surveys in Pure and Applied Mathematics 38 (Longman Scientific & Technical, Harlow, 1995).Google Scholar
[12]Thomassen, C., ‘The rendezvous number of a symmetric matrix and a compact connected metric space’, Amer. Math. Monthly 107 (2000), 163–166.Google Scholar
[13]Wolf, R., ‘On the average distance property of spheres in Banach spaces’, Arch. Math. 62 (1994), 338–344.CrossRefGoogle Scholar
[14]Wolf, R., ‘On the average distance property in finite dimensional real Banach spaces’, Bull. Austral. Math. Soc. 51 (1994), 87–101.CrossRefGoogle Scholar
[15]Wolf, R., ‘Averaging distances in certain Banach spaces’, Bull. Austral. Mat. Soc. 55 (1997), 147–160.Google Scholar
[16]Wolf, R., ‘On the average distance property and certain energy integrals’, Ark. Mat. 35 (1997), 387–400.CrossRefGoogle Scholar
[17]Wolf, R., ‘Averaging distances in real quasihypermetric Banach spaces of finite dimension’, Israel J. Math. 110 (1999), 125–151.CrossRefGoogle Scholar
[18]Wolf, R., ‘On the existence of certain measures appearing in distance geometry’, Arch. Mat. 76 (2001), 308–313.Google Scholar
You have
Access