Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T15:54:37.706Z Has data issue: false hasContentIssue false
  • English
  • Français

MAXIMAL HARDY SPACES ASSOCIATED TO NONNEGATIVE SELF-ADJOINT OPERATORS

Part of: Harmonic analysis in several variables Parabolic equations and systems

Published online by Cambridge University Press:  23 December 2014

GUORONG HU
GUORONG HU*
Affiliation:
Graduate School of Mathematical Sciences, The University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo 153-8914, Japan email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 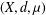$(X,d,{\it\mu})$ be a metric measure space satisfying the doubling, reverse doubling and noncollapsing conditions. Let 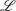$\mathscr{L}$ be a nonnegative self-adjoint operator on 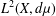$L^{2}(X,d{\it\mu})$ satisfying a pointwise Gaussian upper bound estimate and Hölder continuity for its heat kernel. In this paper, we introduce the Hardy spaces 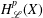$H_{\mathscr{L}}^{p}(X)$, 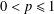$0<p\leq 1$, associated to 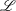$\mathscr{L}$ in terms of grand maximal functions and show that these spaces are equivalently characterised by radial and nontangential maximal functions.

Keywords

Hardy spacesmetric measure spacesself-adjoint operatorsGaussian heat kernel boundsmaximal functions

MSC classification

Primary: 42B30: $H^p$-spaces
Secondary: 42B35: Function spaces arising in harmonic analysis 35K08: Heat kernel
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 286 - 302
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Auscher, P., Duong, X. T. and McIntosh, A., ‘Boundedness of Banach space valued singular integral operators and Hardy spaces’, unpublished manuscript, 2004.Google Scholar
Auscher, P., McIntosh, A. and Russ, E., ‘Hardy spaces of differential forms on Riemannian manifolds’, J. Geom. Anal. 18 (2008), 192–248.Google Scholar
Coulhon, T., Kerkyacharian, G. and Petrushev, P., ‘Heat kernel generated frames in the setting of Dirichlet spaces’, J. Fourier Anal. Appl. 18 (2012), 995–1066.CrossRefGoogle Scholar
Dekel, S., Kerkyacharian, G., Kyriazis, G. and Petrushevl, P., ‘Hardy spaces associated with nonnegative self-adjoint operators’, Preprint, arXiv:1409.0424.Google Scholar
Duong, X. T. and Yan, L., ‘Duality of Hardy and BMO spaces associated with operators with heat kernel bounds’, J. Amer. Math. Soc. 18 (2005), 943–973.CrossRefGoogle Scholar
Duong, X. T. and Yan, L., ‘New function spaces of BMO type, the John–Nirenberg inequality, interpolation, and applications’, Comm. Pure Appl. Math. 58 (2005), 1375–1420.Google Scholar
Dziubański, J., Garrigós, G., Martínez, T., Torrea, J. L. and Zienkiewicz, J., ‘B M O spaces related to Schrödinger operators with potentials satisfying a reverse Hölder inequality’, Math. Z. 249 (2005), 329–356.CrossRefGoogle Scholar
Dziubański, J. and Preisner, M., ‘On Riesz transforms characterization of H 1 spaces associated with some Schrödinger operators’, Potential Anal. 35 (2011), 39–50.Google Scholar
Dziubański, J. and Zienkiewicz, J., ‘Hardy space H 1 associated to Schrödinger operator with potential satisfying reverse Hölder inequality’, Rev. Mat. Iberoam. 15 (1999), 279–296.CrossRefGoogle Scholar
Dziubański, J. and Zienkiewicz, J., ‘H p spaces for Schrödinger operators’, in: Fourier Analysis and Related Topics (Bpolhk edlewo, 2000), Banach Center Publications, 56 (Polish Academy of Science, Warsaw, 2002), 45–53.Google Scholar
Fefferman, C. and Stein, E. M., ‘H p spaces of several variables’, Acta Math. 129 (1972), 137–193.Google Scholar
Folland, G. B. and Stein, E. M., Hardy Spaces on Homogeneous Groups (Princeton University Press, Princeton, NJ, 1982).Google Scholar
Hofmann, S., Lu, G., Mitrea, D., Mitrea, M. and Yan, L., ‘Hardy spaces associated to nonnegative self-adjoint operators satisfying Davies–Gaffney estimates’, Mem. Amer. Math. Soc. 214 (2011), 1–78.Google Scholar
Hofmann, S. and Mayboroda, S., ‘Hardy and BMO spaces associated to divergence form elliptic operators’, Math. Ann. 344 (2009), 37–116.Google Scholar
Jiang, R., Jiang, X. and Yang, D., ‘Maximal function characterizations of Hardy spaces associated with Schrödinger operators on nilpotent Lie groups’, Rev. Mat. Complut. 24 (2011), 251–275.Google Scholar
Kerkyacharian, G. and Petrushev, P., ‘Heat kernel based decomposition of spaces of distributions in the framework of Dirichlet spaces’, Trans. Amer. Math. Soc. 367 (2015), 121–189.Google Scholar
Stein, E. M., Harmonic Analysis: Real-variable Methods, Orthogonality, and Oscillatory Integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Stein, E. M. and Weiss, G., ‘On the theory of harmonic functions of several variables. I. The theory of H p-spaces’, Acta Math. 103 (1960), 25–62.CrossRefGoogle Scholar