Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2025-01-03T18:05:06.667Z Has data issue: false hasContentIssue false
  • English
  • Français

The log log law for multidimensional stochastic integrals and diffusion processes

Published online by Cambridge University Press:  17 April 2009

Ludwig Arnold
Ludwig Arnold
Affiliation:
Centre de recherches mathématiques, Université de Montréal, Montréal, Canada.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let for t ∈ [a, b] ⊂ [0, ∞)

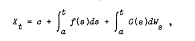where Ws is an n-dimensional Wiener process, f(s) an n-vector process and G(s) an n × m matrix process. f and G are nonanticipating and sample continuous. Then the set of limit points of the net

in Rn is equal, almost surely, to the random ellipsoid Et = G(t)Sm, Sm = {x ∈ Rm: |x| ≤ 1}. The analogue of Lévy's law is also given. The results apply to n-dimensional diffusion processes which are solutions of stochastic differential equations, thus extending the versions of Hinčin's and Lévy's laws proved by H.P. McKean, Jr, and W.J. Anderson.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 5 , Issue 3 , December 1971 , pp. 351 - 356
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Anderson, William James, “Local behaviour of solutions of stochastic integral equations”, (Ph.D. thesis, McGill University, Montreal, 1969).Google Scholar
[2]Gikhman, I.I., Skorokhod, A.V., Introduction to the theory of random processes (Sounders, Philadelphia, London, Toronto, 1969).Google Scholar
[3]McKean, H.P. Jr, Stochastic integrals (Academic Press, New York, London, 1969).Google Scholar