Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T01:09:26.088Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL RADIAL BASIS FUNCTION APPROXIMATION ON THE SPHERE

Part of: Approximations and expansions Numerical approximation and computational geometry

Published online by Cambridge University Press:  01 April 2008

KERSTIN HESSE  and
Q. T. LE GIA
KERSTIN HESSE
Affiliation:
Department of Mathematics, Mantell Building, University of Sussex, Falmer, Brighton BN1 9RF, UK (email: [email protected])
Q. T. LE GIA
Affiliation:
School of Mathematics and Statistics, The University of New South Wales, Sydney NSW 2052, Australia (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we derive local error estimates for radial basis function interpolation on the unit sphere 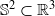. More precisely, we consider radial basis function interpolation based on data on a (global or local) point set 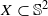for functions in the Sobolev space 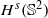with norm 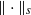, where s>1. The zonal positive definite continuous kernel ϕ, which defines the radial basis function, is chosen such that its native space can be identified with 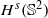. Under these assumptions we derive a local estimate for the uniform error on a spherical cap S(z;r): the radial basis function interpolant ΛXf of 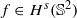satisfies 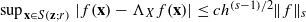, where h=hX,S(z;r) is the local mesh norm of the point set X with respect to the spherical cap S(z;r). Our proof is intrinsic to the sphere, and makes use of the Videnskii inequality. A numerical test illustrates the theoretical result.

Keywords

error estimateinterpolationlocal approximationmesh normnative spacepositive definite kernelradial basis functionreproducing kernelSobolev spacespherespherical capVidenskii inequality

MSC classification

Secondary: 41A05: Interpolation 41A15: Spline approximation 41A25: Rate of convergence, degree of approximation 65D05: Interpolation 65D07: Splines
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 77 , Issue 2 , April 2008 , pp. 197 - 224
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Aronszajn, N., ‘Theory of reproducing kernels’, Trans. Amer. Math. Soc. 68 (1950), 337–404.CrossRefGoogle Scholar
[2]Borwein, P. and Erdélyi, T., Polynomials and polynomial inequalities (Springer, New York, 1995).CrossRefGoogle Scholar
[3]Chen, D., Menegatto, V. A. and Sun, X., ‘A necessary and sufficient condition for strictly positive definite functions on spheres’, Proc. Amer. Math. Soc. 131 (2003), 2733–2740.CrossRefGoogle Scholar
[4]Freeden, W., Gervens, T. and Schreiner, M., Constructive approximation on the sphere (with applications to geomathematics) (Clarendon Press, Oxford, 1998).CrossRefGoogle Scholar
[5]Golitschek, M. V. and Light, W. A., ‘Interpolation by polynomials and radial basis functions on spheres’, Constr. Approx. 17 (2001), 1–18.CrossRefGoogle Scholar
[6]Hubbert, S. and Morton, T. M., ‘L p-error estimates for radial basis function interpolation on the sphere’, J. Approx. Theory 129 (2004), 58–77.CrossRefGoogle Scholar
[7]Jetter, K., Stöckler, J. and Ward, J. D., ‘Error estimates for scattered data interpolation on spheres’, Math. Comp. 68 (1999), 733–747.CrossRefGoogle Scholar
[8]Le Gia, Q. T., Narcowich, F. J., Ward, J. D. and Wendland, H., ‘Continuous and discrete least-squares approximation by radial basis functions on spheres’, J. Approx. Theory 143 (2006), 124–133.CrossRefGoogle Scholar
[9]Levesley, J., Light, W., Ragozin, D. and Sun, X., ‘A simple approach to the variational theory for interpolation on spheres’, in: New developments in approximation theory, International Series of Numerical Mathematics, 132 (eds. M. W. Müller, M. D. Buhmann, D. H. Mache and M. Felten) (Birkhäuser, Basel, 1999), pp. 109–116.Google Scholar
[10]Morton, T. M. and Neamtu, M., ‘Error bounds for solving pseudodifferential equations on spheres by collocation with zonal kernels’, J. Approx. Theory 114 (2002), 242–268.CrossRefGoogle Scholar
[11]Narcowich, F. J. and Ward, J. D., ‘Scattered data interpolation on spheres: error estimates and locally supported basis functions’, SIAM J. Math. Anal. 33 (2002), 1393–1410.CrossRefGoogle Scholar
[12]Ratcliffe, J. R., Foundations of hyperbolic manifolds (Springer, New York, 1994).CrossRefGoogle Scholar
[13]Reimer, M., Multivariate polynomial approximation, International Series of Numerical Mathematics, 144 (Birkhäuser, Basel, 2003).CrossRefGoogle Scholar
[14]Saff, E. B. and Kuijlaars, A. B. J., ‘Distributing many points on a sphere’, Math. Intelligencer 19 (1997), 5–11.CrossRefGoogle Scholar
[15]Schoenberg, I. J., ‘Positive definite functions on the spheres’, Duke Math. J. 9 (1942), 96–108.CrossRefGoogle Scholar
[16]Szegö, G., Orthogonal polynomials, American Mathematical Society Colloquium Publications, 23 (American Mathematical Society, Providence, RI, 1975).Google Scholar
[17]Wendland, H., ‘Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree’, Adv. Comput. Math. 4 (1995), 389–396.CrossRefGoogle Scholar
[18]Wendland, H., Scattered data approximation, Cambridge Monographs on Applied and Computational Mathematics, 17 (Cambridge University Press, Cambridge, 2005).Google Scholar
[19]Xu, Y. and Cheney, E. W., ‘Strictly positive definite functions on spheres’, Proc. Amer. Math. Soc. 116 (1992), 977–981.CrossRefGoogle Scholar