Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T18:55:41.146Z Has data issue: false hasContentIssue false
  • English
  • Français

LIPSCHITZ SPACES AND BOUNDED MEAN OSCILLATION OF HARMONIC MAPPINGS

Part of: Geometric function theory Spaces and algebras of analytic functions

Published online by Cambridge University Press:  18 January 2013

SH. CHEN ,
S. PONNUSAMY ,
M. VUORINEN  and
X. WANG
SH. CHEN
Affiliation:
Department of Mathematics and Computational Science, Hengyang Normal University, Hengyang, Hunan 421008,PR China email [email protected]
S. PONNUSAMY*
Affiliation:
Indian Statistical Institute (ISI), Chennai Centre, SETS (Society for Electronic Transactions and Security), MGR Knowledge City, CIT Campus, Taramani, Chennai 600 113, India
M. VUORINEN
Affiliation:
Department of Mathematics, University of Turku, Turku 20014, Finland email [email protected]
X. WANG
Affiliation:
Department of Mathematics, Hunan Normal University, Changsha, Hunan 410081,PR China email [email protected]
*
✉[email protected][email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We first study the bounded mean oscillation of planar harmonic mappings. Then we establish a relationship between Lipschitz-type spaces and equivalent modulus of real harmonic mappings. Finally, we obtain sharp estimates on the Lipschitz number of planar harmonic mappings in terms of the bounded mean oscillation norm, which shows that the harmonic Bloch space is isomorphic to 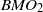$BM{O}_{2} $ as a Banach space.

Keywords

harmonic mappingmajorantLipschitz spaceBMOpequivalent modulusharmonic Bloch spaceGreen’s theorem

MSC classification

Secondary: 30H10: Hardy spaces 30H30: Bloch spaces 30C20: Conformal mappings of special domains 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 143 - 157
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Arsenović, M., Boz˘in, V. and Manojlović, V., ‘Moduli of continuity of harmonic quasiregular mappings in ${ \mathbb{B} }^{n} $’, Potential Anal. 34 (2011), 283–291.CrossRefGoogle Scholar
Chen, Sh., Ponnusamy, S. and Wang, X., ‘Bloch constant and Landau’s theorems for planar p-harmonic mappings’, J. Math. Anal. Appl. 373 (2011), 102–110.CrossRefGoogle Scholar
Chen, Sh., Ponnusamy, S. and Wang, X., ‘Landau’s theorem and Marden constant for harmonic $\nu $-Bloch mappings’, Bull. Aust. Math. Soc. 84 (2011), 19–32.CrossRefGoogle Scholar
Chen, Sh., Ponnusamy, S. and Wang, X., ‘On planar harmonic Lipschitz and planar harmonic Hardy classes’, Ann. Acad. Sci. Fenn. Math. 36 (2011), 567–576.CrossRefGoogle Scholar
Chen, Sh., Ponnusamy, S. and Wang, X., ‘Integral means and coefficient estimates on planar harmonic mappings’, Ann. Acad. Sci. Fenn. Math. 37 (2012), 69–79.CrossRefGoogle Scholar
Chen, Sh., Ponnusamy, S. and Wang, X., ‘Area integral means, Hardy and weighted Bergman spaces on planar harmonic mappings’, Kodai Math. J., to appear, http://arxiv.org/abs/1203.2711.Google Scholar
Chen, Sh., Ponnusamy, S. and Wang, X., ‘Equivalent moduli of continuity, Bloch’s theorem for pluriharmonic mappings in ${ \mathbb{B} }^{n} $’, Proc. Indian Acad. Sci. Math. Sci. 122 (4) (2012), 583–595.CrossRefGoogle Scholar
Chen, Sh. and Wang, X., ‘On harmonic Bloch spaces in the unit ball of ${ \mathbb{C} }^{n} $’, Bull. Aust. Math. Soc. 84 (2011), 67–78.CrossRefGoogle Scholar
Clunie, J. G. and MacGregor, T. H., ‘Radial growth of the derivative of univalent functions’, Comment. Math. Helv. 59 (1984), 362–375.CrossRefGoogle Scholar
Clunie, J. G. and Sheil-Small, T., ‘Harmonic univalent functions’, Ann. Acad. Sci. Fenn. Ser. A I Math. 9 (1984), 3–25.CrossRefGoogle Scholar
Coifman, R. R., Rochberg, R. and Weiss, G., ‘Factorization theorems for Hardy spaces in several complex variables’, Ann. of Math. (2) 103 (1976), 611–635.CrossRefGoogle Scholar
Colonna, F., ‘The Bloch constant of bounded harmonic mappings’, Indiana Univ. Math. J. 38 (1989), 829–840.CrossRefGoogle Scholar
Duren, P., Harmonic Mappings in the Plane (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Dyakonov, K. M., ‘Equivalent norms on Lipschitz-type spaces of holomorphic functions’, Acta Math. 178 (1997), 143–167.CrossRefGoogle Scholar
Dyakonov, K. M., ‘Holomorphic functions and quasiconformal mappings with smooth moduli’, Adv. Math. 187 (2004), 146–172.CrossRefGoogle Scholar
Fefferman, C. and Stein, E. M., ‘${H}^{p} $ spaces of several variables’, Acta Math. 129 (1972), 137–193.CrossRefGoogle Scholar
Gehring, F. W. and Martio, O., ‘Lipschitz-classes and quasiconformal mappings’, Ann. Acad. Sci. Fenn. Ser. A I Math. 10 (1985), 203–219.CrossRefGoogle Scholar
Hahn, K. T. and Youssfi, E. H., ‘$ \mathcal{M} $-harmonic Besov $p$-spaces and Hankel operators in the Bergman space on the ball in ${ \mathbb{C} }^{n} $’, Manuscripta Math. 71 (1991), 67–81.CrossRefGoogle Scholar
Hall, R. R., ‘On an inequality of E. Heinz’, J. Anal. Math. 42 (1982/83), 185–198.CrossRefGoogle Scholar
Hayman, W. K. and Pommerenke, Ch., ‘On analytic functions of bounded mean oscillation’, Bull. Lond. Math. Soc. 10 (1978), 214–224.CrossRefGoogle Scholar
Jevtić, M., ‘$ \mathcal{M} $-harmonic Bloch space and $BMO$ in the Bergman metric on the ball’, Zb. Rad. 6 (1992), 83–88.Google Scholar
Kalaj, D. and Vuorinen, M., ‘On harmonic functions and the Schwarz lemma’, Proc. Amer. Math. Soc. 140 (2012), 161–165.CrossRefGoogle Scholar
Kojić, V. and Pavlović, M., ‘Subharmonicity of $\vert f\mathop{\vert }\nolimits ^{p} $ for quasiregular harmonic functions, with applications’, J. Math. Anal. Appl. 342 (2008), 742–746.CrossRefGoogle Scholar
Korenblum, B., ‘BMO estimates and radial growth of Bloch functions’, Bull. Amer. Math. Soc. 12 (1985), 99–102.CrossRefGoogle Scholar
Lappalainen, V., ‘${\mathrm{Lip} }_{h} $-extension domains’, Ann. Acad. Sci. Fenn. Ser. A I Math. Diss. 56 (1985).Google Scholar
Mateljević, M., ‘Quasiconformal and quasiregular harmonic analogues of Koebe’s theorem and applications’, Ann. Acad. Sci. Fenn. Math. 32 (2007), 301–315.Google Scholar
Mateljević, M. and Vuorinen, M., ‘On harmonic quasiconformal quasi-isometries’, J. Inequal. Appl. 2010, Article ID 178732, 19 pages, doi:10.1155/2010/1787.Google Scholar
Pavlović, M., ‘On Dyakonov’s paper equivalent norms on Lipschitz-type spaces of holomorphic functions’, Acta Math. 183 (1999), 141–143.CrossRefGoogle Scholar
Pavlović, M., Introduction to Function Spaces on the Disk, Matematic˘ki Institut SANU, Belgrade, 2004.Google Scholar
Pavlović, M., ‘Lipschitz conditions on the modulus of a harmonic function’, Rev. Mat. Iberoam. 23 (2007), 831–1845.CrossRefGoogle Scholar
Pavlović, M., ‘A Schwarz lemma for the modulus of a vector-valued analytic function’, Proc. Amer. Math. Soc. 139 (2011), 969–973.CrossRefGoogle Scholar
Pommerenke, Ch., Boundary Behaviour of Conformal Maps (Springer, Berlin, 1992).CrossRefGoogle Scholar
Qiao, J. and Wang, X., Lipschitz-type spaces of pluriharmonic mappings, Filomat, to appear.Google Scholar
Sheil-Small, T., ‘Constants for planar harmonic mappings’, J. Lond. Math. Soc. 42 (1990), 237–248.CrossRefGoogle Scholar
Vuorinen, M., Conformal Geometry and Quasiregular Mappings, Lecture Notes in Mathematics, 1319 (Springer, Berlin, 1988), 209pp.CrossRefGoogle Scholar
Vuorinen, M., ‘Geometry of metrics’, J. Anal. 18 (2010), 399–424.Google Scholar