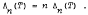Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T06:22:30.393Z Has data issue: false hasContentIssue false
  • English
  • Français

A link between Lebesgue constants and Hermite-Fejér interpolation

Published online by Cambridge University Press:  17 April 2009

S. J. Goodenough
S. J. Goodenough
Affiliation:
Department of Mathematics, Statistics, Computer Science, University of Newcastle, N.S.W. 2308.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A review of the development of estimates for Lebesgue constants associated with Lagrange interpolation on the one hand, and estimates for the rate of convergence of Hermite-Fejér interpolation on the other hand, provides a historical perspective for the following surprising, close link between these apparently diverse concepts. Denoting by Λn (T) the Lebesgue constant of order n and by Δn (T) the maximum interpolation error for functions of class Lip 1 by Hexmite-Fejér interpolation polynomials of degree not exceeding 2n − 1, based on the zeros of the Chebyshev polynomial of first kind, we discover that, for even values of n, Λn(T) = n Δn(T).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 33 , Issue 2 , April 1986 , pp. 207 - 218
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Berman, D.L., “On the best grid system for parabolic interpolation” (Russian), Izv. Vyss. Učebn. Zaved. Matematika 4 (1963), 20–25.Google Scholar
[2]Bernstein, S.N., “Quelques remarques sur l'interpolation”, Communic. Math. Assoc. Kharkov 15 (1916), 49–61.Google Scholar
[3]Bernstein, S.N., “Sur la limitation des valeurs d'une polynôme P (x) de degré n sur tout un segment par ses valeurs en (n+1) points du segment” Izv. Akad. Nauk SSSR 7 (1931), 1025–1050.Google Scholar
[4]Bojanic, R., “A note on the precision of interpolation by Hermite-Fejér polynomials”,Proceedings of the Conference on constructive theory of functions, Budapest1969,69–76 (Akadémiai Kiadó, Budapest, 1972).Google Scholar
[5]De Vore, R.A., The approximation of continuous functions by positive linear operators (Lecture Notes in Mathematics 293. Springer-Verlag, Barlin, Heidelberg, New York, 1972).CrossRefGoogle Scholar
[6]Ehlich, H. and Zeller, K., “Auswertung der Normen von Interpolations-operatoren”, Math. Ann. 164 (1966), 105–112.CrossRefGoogle Scholar
[7]Fejér, L., “Ueber Interpolation”, Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. (1916), 66–91.Google Scholar
[8]Goodenough, S.J., “The complete asymptotic expansion for the degree of approximation of Lipschitz functions by Hermite-Fejér interpolation polynomials” J. Approx. Theory 44 (1985), 325–342.CrossRefGoogle Scholar
[9]Goodenough, S.J., Error estimates for the approximation of functions by certain interpolation polynomials (ph.D. thesis, University of Newcastle, 1985).Google Scholar
[10]Goodenough, S.J. and Mills, T.M., “A new estimate for the approximation of functions by Hermite-Fejér interpolation polynomials”, J. Approx. Theory 31 (1981), 253–260.CrossRefGoogle Scholar
[11]Günttner, R., Abschätzungen für Normen von Interpolationsoperatoren (Doctoral dissertation, Technical University of Clausthal, West Germany, 1972).Google Scholar
[12]Günttner, R., “Evaluation of Lebesgue constants”, SIAM J. Numer. Anal. 17 (1980), 512–520.CrossRefGoogle Scholar
[13]Luttman, F.W. and Rivlin, T.J., “Some numerical experiments in the theory of polynomial interpolation”, IBM J. Res. Develop. 2 (1965), 187–191.CrossRefGoogle Scholar
[14]Mills, T.M., “Some techniques in approximation theory”, Math. Scientist 5 (1980), 105–120.Google Scholar
[15]Moldovan, E., “Observatii asupra unor procedee de interpolare generalizate”, Acad. Repub. Pop. Rom. Bul. Stinte Sect. Stinte Mat. Fiz. 6 (1954), 477–482.Google Scholar
[16]Natanson, I.P., Constructive function theory, Vol. III (Frederick Ungar, New York, 1965).Google Scholar
[17]Popoviciu, T., “Asupra demonstratiei teoremai lui Weierstrass cu ajutorul polynoamelor de interpolare”, Acad. Repub. Pop. Rom., Lucrarile sessiunii generala ştintifice din 2–12 iunie, 1950 (1951), 1664–1667.Google Scholar
[18]Powell, M.J.D., “On the maximum errors of polynomial approximations defined by interpolation and by least squares criteria”, Comput. J. 9 (1967), 404–407.CrossRefGoogle Scholar
[19]Rivlin, T.J., “The Lebesgue constants for polynomial interpolation”, Functional Analysis and its Applications, Int. Conf. Madrass 1973, 422–437 (Springer-Verlag, Berlin, 1974).Google Scholar
[20]Rovlin, T.J., The Chebyshev polynomials (Wiley-Interscience, New York, London, Sydney, Toronto, 1974).Google Scholar
[21]Saxena, R.B., “A note on the rate of convergence of Hermite-Fejér interpolation Polynomials”, Canad. Math. Bull. 17 (1974), 299–301.CrossRefGoogle Scholar
[22]Shisha, O. and Mond, B., “The rapidity of convergence of the Hermite-Fejér approximation to functions of one or several variables”, Proc. Amer. Math. Soc. 16 (1965), 1269–1276.Google Scholar
[23]Shivakumar, P.N. and Wong, R., “Asymptotic expansion of the Lebesgue constants associated with polynomial interpolation”, Math. Comp. 39 (1982), 195–200.CrossRefGoogle Scholar
[24]Vértesi, P.O.H., “On the convergence of Hermite-Fejér interpolation”, Acta Math. Acad. Sci. Hungar. 22 (1971), 151–158.CrossRefGoogle Scholar