Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T03:04:21.755Z Has data issue: false hasContentIssue false
  • English
  • Français

LINEAR INDEPENDENCE OF POWERS OF SINGULAR MODULI OF DEGREE THREE

Part of: Diophantine approximation, transcendental number theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  12 September 2018

FLORIAN LUCA Open the ORCID record for FLORIAN LUCA [Opens in a new window]  and
ANTONIN RIFFAUT Open the ORCID record for ANTONIN RIFFAUT [Opens in a new window]
FLORIAN LUCA
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag X3, Wits 2050, Johannesburg, South Africa Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany Department of Mathematics, Faculty of Sciences, University of Ostrava, 30 dubna 22, 701 03 Ostrava 1, Czech Republic email [email protected]
ANTONIN RIFFAUT*
Affiliation:
Institut de Mathématiques de Bordeaux, Université de Bordeaux, A33, 351 Cours de la Libération, 33400 Talence, France email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that two distinct singular moduli 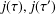$j(\unicode[STIX]{x1D70F}),j(\unicode[STIX]{x1D70F}^{\prime })$, such that for some positive integers 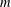$m$ and $n$ the numbers 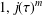$1,j(\unicode[STIX]{x1D70F})^{m}$ and 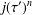$j(\unicode[STIX]{x1D70F}^{\prime })^{n}$ are linearly dependent over 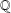$\mathbb{Q}$, generate the same number field of degree at most two. This completes a result of Riffaut [‘Equations with powers of singular moduli’, Int. J. Number Theory, to appear], who proved the above theorem except for two explicit pairs of exceptions consisting of numbers of degree three. The purpose of this article is to treat these two remaining cases.

Keywords

linear independencesingular modulilinear forms in two logarithms

MSC classification

Primary: 11J20: Inhomogeneous linear forms
Secondary: 11F03: Modular and automorphic functions 11J61: Approximation in non-Archimedean valuations 11J86: Linear forms in logarithms; Baker's method
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 42 - 50
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Allombert, B., Bilu, Yu. and Pizarro-Madariaga, A., ‘CM-points on straight lines’, in: Analytic Number Theory in Honor of Helmut Maier’s 60th Birthday (eds. Pomerance, C. and Rassias, M. T.) (Springer, Cham, Switzerland, 2015), 1–18.Google Scholar
André, Y., ‘Finitudes des couples d’invariants modulaires singuliers sur une courbe algébrique plane non modulaire’, J. reine angew. Math. 505 (1998), 203–208.Google Scholar
Bilu, Yu., Hanrot, G., Voutier, P. M. and Mignotte, M., ‘Existence of primitive divisors of Lucas and Lehmer numbers’, J. reine angew. Math. 539 (2001), 75–122.Google Scholar
Bilu, Yu., Luca, F. and Pizarro-Madariaga, A., ‘Rational products of singular moduli’, J. Number Theory 158 (2016), 397–410.Google Scholar
Bilu, Yu., Masser, D. and Zannier, U., ‘An effective “Theorem of André” for CM-points on a plane curve’, Math. Proc. Cambridge Philos. Soc. 154 (2013), 145–152.Google Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine Geometry (Cambridge University Press, Cambridge, 2006).Google Scholar
Cox, D. A., Primes of the Form x 2 + ny 2 (Wiley, New York, 1989).Google Scholar
Kühne, L., ‘An effective result of André–Oort type II’, Acta Arith. 161 (2013), 1–19.Google Scholar
Laurent, M., Mignotte, M. and Nesterenko, Y., ‘Formes linéaires en deux logarithmes et déterminants d’interpolation’, J. Number Theory 55 (1995), 285–321.Google Scholar
Riffaut, A., ‘Equations with powers of singular moduli’, Int. J. Number Theory (to appear), arXiv:1710.03547.Google Scholar
The PARI Group, PARI/GP, version 2.7.1 (2014), Bordeaux; available fromhttp://pari.math.u-bordeaux.fr/.Google Scholar