No CrossRef data available.
Published online by Cambridge University Press: 06 October 2023
The lifting problem for universal quadratic forms over a totally real number field K consists of determining the existence or otherwise of a quadratic form with integer coefficients (or 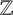 $\mathbb {Z}$-form) that is universal over K. We prove the nonexistence of universal
$\mathbb {Z}$-form) that is universal over K. We prove the nonexistence of universal 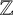 $\mathbb {Z}$-forms over simplest cubic fields for which the integer parameter is big enough. The monogenic case is already known. We prove the nonexistence in the nonmonogenic case by using the existence of a totally positive nonunit algebraic integer in K with minimal (codifferent) trace equal to one.
$\mathbb {Z}$-forms over simplest cubic fields for which the integer parameter is big enough. The monogenic case is already known. We prove the nonexistence in the nonmonogenic case by using the existence of a totally positive nonunit algebraic integer in K with minimal (codifferent) trace equal to one.
The first author was supported by Czech Science Foundation GAČR, grant 21-00420M, and by Charles University Research Centre program UNCE/SCI/022. The second author was supported by Czech Science Foundation GAČR, grant 22-11563O.