Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T16:53:18.422Z Has data issue: false hasContentIssue false
  • English
  • Français

LIFTING HOMEOMORPHISMS AND FINITE ABELIAN BRANCHED COVERS OF THE 2-SPHERE

Part of: Low-dimensional topology

Published online by Cambridge University Press:  02 June 2022

HAIMIAO CHEN Open the ORCID record for HAIMIAO CHEN [Opens in a new window]
HAIMIAO CHEN*
Affiliation:
Department of Mathematics, Beijing Technology and Business University, Beijing, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We completely determine finite abelian regular branched covers of the 2-sphere 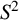$S^{2}$ with the property that each homeomorphism of 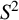$S^{2}$ preserving the branching set can be lifted.

Keywords

abelian branched cover2-spherelifting homeomorphism

MSC classification

Primary: 57M12: Special coverings, e.g. branched
Secondary: 57M60: Group actions in low dimensions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 504 - 507
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atalan, F., Medetogullari, E. and Ozan, Y., ‘Liftable homeomorphisms of rank two finite abelian branched covers’, Arch. Math. 116 (2021), 37–48.10.1007/s00013-020-01501-zCrossRefGoogle Scholar
Birman, J. S. and Hilden, H. M., ‘Erratum to “Isotopies of homeomorphisms of Riemann surfaces”’, Ann. of Math. (2) 185(1) (2017), 345.10.4007/annals.2017.185.1.9CrossRefGoogle Scholar
Chen, H.-M. and Shen, H., ‘How to find G-admissible coverings of a graph?’, Linear Algebra Appl. 438(8) (2015), 3303–3320.10.1016/j.laa.2012.12.041CrossRefGoogle Scholar
Ghaswala, T. and Winarski, R. R., ‘Lifting homeomorphisms and cyclic branched covers of spheres’, Michigan Math. J. 66 (2017), 885–890.10.1307/mmj/1508810819CrossRefGoogle Scholar
Margalit, D. and Winarski, R. R., ‘Braids groups and mapping class groups: the Birman–Hilden theory’, Bull. Lond. Math. Soc. 53 (2021), 643–659.10.1112/blms.12456CrossRefGoogle Scholar