Hostname: page-component-5f56664f6-c65qm Total loading time: 0 Render date: 2025-05-08T02:18:19.161Z Has data issue: false hasContentIssue false
  • English
  • Français

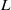$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES

Part of: Sequences and sets Multiplicative number theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  22 March 2013

FLORIAN LUCA ,
ROGER OYONO  and
AYNUR YALCINER
FLORIAN LUCA*
Affiliation:
Fundación Marcos Moshinsky, Instituto de Ciencias Nucleares UNAM, Circuito Exterior, C.U., Apdo. Postal 70-543, Mexico D.F. 04510, Mexico
ROGER OYONO
Affiliation:
Équipe GAATI, Université de la Polynésie Française, BP 6570, 98702 Faa’a, Tahiti, French Polynesia email [email protected]
AYNUR YALCINER
Affiliation:
Department of Mathematics, Faculty of Science, Selçuk University, Campus 42075 Konya, Turkey email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 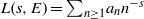$L(s, E)= {\mathop{\sum }\nolimits}_{n\geq 1} {a}_{n} {n}^{- s} $ be the 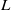$L$-series corresponding to an elliptic curve 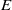$E$ defined over 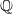$ \mathbb{Q} $ and 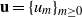$\mathbf{u} = \mathop{\{ {u}_{m} \} }\nolimits_{m\geq 0} $ be a nondegenerate binary recurrence sequence. We prove that if 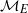${ \mathcal{M} }_{E} $ is the set of $n$ such that 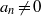${a}_{n} \not = 0$ and 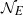${ \mathcal{N} }_{E} $ is the subset of 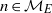$n\in { \mathcal{M} }_{E} $ such that 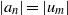$\vert {a}_{n} \vert = \vert {u}_{m} \vert $ holds with some integer 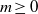$m\geq 0$, then 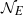${ \mathcal{N} }_{E} $ is of density 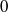$0$ as a subset of 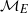${ \mathcal{M} }_{E} $.

Keywords

L-functions of elliptic curveslinear recurrence sequences

MSC classification

Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 11B39: Fibonacci and Lucas numbers and polynomials and generalizations 11N36: Applications of sieve methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 509 - 519
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Canfield, E. R., Erdős, P. and Pomerance, C., ‘On a problem of Oppenheim concerning factorisatio numerorum’, J. Number Theory 17 (1983), 1–28.CrossRefGoogle Scholar
Cojocaru, A. C., ‘Questions about the reductions modulo primes of an elliptic curve’, in: Number Theory: Proceedings of the 7th Conference of the Canadian Number Theory Association (Montreal, 2002), CRM Proceedings and Lecture Notes, 36 (eds. Kisilevsky, H. and Goren, E.) (American Mathematical Society, Providence, RI, 2004), 61–79.Google Scholar
Deuring, M., ‘Die Typen der Multiplikatorenringe elliptischer Functionenkörper’, Abh. Math. Sem. Hansischen Univ. 14 (1941), 197–272.CrossRefGoogle Scholar
Elkies, N. D., ‘The existence of infinitely many supersingular primes for every elliptic curve over $ \mathbb{Q} $’, Invent. Math. 89 (1987), 561–567.CrossRefGoogle Scholar
Hall, R. R. and Tenenbaum, G., Divisors (Cambridge University Press, Cambridge, 1988).Google Scholar
Luca, F. and Yalçiner, A., ‘$L$-functions of elliptic curves and Fibonacci numbers’, Fibonacci Quart. to appear.Google Scholar
Lucas, E., ‘Théorie des fonctions numériques simplement périodiques’, Amer. J. Math. 1 (1878), 189–240; 289–321.CrossRefGoogle Scholar
Serre, J.-P., ‘Quelques applications du théorème de densité de Chebotarev’, Publ. Math. Inst. Hautes Études Sci. 54 (1981), 123–201.Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves (Springer-Verlag, Berlin, 1995).Google Scholar
Somer, L., ‘Which second-order linear integral recurrences have almost all primes as divisors?’, Fibonacci Quart. 17 (1979), 111–116.Google Scholar
Stewart, C. L., Divisor Properties of Arithmetical Sequences, PhD Thesis, University of Cambridge, 1976.Google Scholar
Wirsing, E., ‘Das asymptotische Verhalten von Summen über multiplikative Funktionen’, Math. Ann. 143 (1961), 75–102.Google Scholar