Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-07-05T15:13:27.506Z Has data issue: false hasContentIssue false
  • English
  • Français

The Kunze–Stein phenomenon on the isometry group of a tree

Published online by Cambridge University Press:  17 April 2009

Alessandro Veca
Alessandro Veca
Affiliation:
Dipartimento di Matematica, Università di Milano, via Saldini 50, 20133 Milano, Italia e-mail: [email protected] School of Mathematics, UNSW, Sydney NSW 2052, Australia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be the group of isometries of a homogeneous tree . In the first part of this paper we decompose G in terms of certain subgroups N, ℤ, and K to obtain the related integral formula

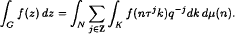
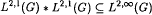Then, by using ideas of A. Ionescu and the formula above, we prove that and that a related maximal operator on  is bounded from L2, 1() to L2,∞(). We finally show that Lp, 1(K\G/K) is a commutative Banach algebra of convolutors for Lp(G) and give an explicit description of its Gelfand spectrum.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 65 , Issue 1 , February 2002 , pp. 153 - 174
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Cowling, M., ‘The Kunze-Stein phenomenon’, Ann. Math. 107 (1978), 209–234.Google Scholar
[2]Cowling, M., ‘Herz's “principe de majoration” and the Kunze-Stein phenomenon’, in Harmonic analysis and number theory (Montreal, PQ, 1996) (Amer. Math. Soc., Providence, RI, 1997), pp. 73–88.Google Scholar
[3]Cowling, M., Meda, S. and Setti, A.G., ‘An overview of harmonic analysis on the group of isometries of a homogeneous tree’, Exposition. Math. 16 (1988), 385–423.Google Scholar
[4]Figà-Talamanca, A. and Nebbia, C., Harmonic analysis and representation theory for groups acting on homogeneous trees (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
[5]Ionescu, A.D., ‘An endpoint estimate for the Kunze-Stein phenomenon and related maximal operator’, Ann. of Math. 152 (2000), 259–275.CrossRefGoogle Scholar
[6]Kunze, R.A. and Stein, E.M., ‘Uniformly bounded representations and harmonic analysis of the 2 × 2 real unimodular group’, Amer. J. Math. 82 (1960), 1–62.CrossRefGoogle Scholar
[7]Lions, J.-L. and Peetre, J., ‘Sur une classe d'espaces d'interpolation’, Inst. Hautes Études Sci. Publ. Math. 19 (1964), 5–68.CrossRefGoogle Scholar
[8]Lohoué, N., ‘Estimations Lp des coefficients de représentataion et opérateurs de convolution’, Adv. in Math. 38 (1980), 178–221.CrossRefGoogle Scholar
[9]Pytlik, T., ‘Radial convolutors on free groups’, Studia Math. 78 (1984), 179–183.CrossRefGoogle Scholar
[10]Stein, E.M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces, Princeton Mathematical Series 32 (Princeton University Press, Princeton, N.J., 1971).Google Scholar