Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
LaLonde, Scott M.
and
Milan, David
2017.
Amenability and uniqueness for groupoids associated with inverse semigroups.
Semigroup Forum,
Vol. 95,
Issue. 2,
p.
321.
Donsig, Allan
Gensler, Jennifer
King, Hannah
Milan, David
and
Wdowinski, Ronen
2020.
On zigzag maps and the path category of an inverse semigroup.
Semigroup Forum,
Vol. 100,
Issue. 3,
p.
790.
Ortega, Eduard
and
Pardo, Enrique
2020.
The tight groupoid of the inverse semigroups of left cancellative small categories.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 7,
p.
5199.
Exel, Ruy
2021.
Operator Theory, Functional Analysis and Applications.
Vol. 282,
Issue. ,
p.
183.
Kudryavtseva, Ganna
2021.
Semigroups, Categories, and Partial Algebras.
Vol. 345,
Issue. ,
p.
71.
Lawson, Mark V.
2021.
Semigroups, Categories, and Partial Algebras.
Vol. 345,
Issue. ,
p.
179.
Laca, Marcelo
and
Sehnem, Camila
2022.
Toeplitz algebras of semigroups.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 10,
p.
7443.
Lawson, Mark V.
Sims, Aidan
and
Vdovina, Alina
2024.
Higher dimensional generalizations of the Thompson groups via higher rank graphs.
Journal of Pure and Applied Algebra,
Vol. 228,
Issue. 1,
p.
107456.
Larki, Hossein
2025.
An inverse semigroup approach to self-similar k-graph $$C^*$$-algebras and simplicity.
Banach Journal of Mathematical Analysis,
Vol. 19,
Issue. 1,
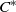 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS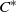 ${C}^{\ast } $-algebra of a finitely aligned category of paths, developed by Spielberg, is the tight
${C}^{\ast } $-algebra of a finitely aligned category of paths, developed by Spielberg, is the tight 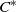 ${C}^{\ast } $-algebra of a natural inverse semigroup. This includes as a special case finitely aligned higher-rank graphs: that is, for such a higher-rank graph
${C}^{\ast } $-algebra of a natural inverse semigroup. This includes as a special case finitely aligned higher-rank graphs: that is, for such a higher-rank graph 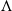 $\Lambda $, the tight
$\Lambda $, the tight 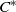 ${C}^{\ast } $-algebra of the inverse semigroup associated to
${C}^{\ast } $-algebra of the inverse semigroup associated to 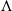 $\Lambda $ is the same as the
$\Lambda $ is the same as the 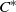 ${C}^{\ast } $-algebra of
${C}^{\ast } $-algebra of 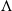 $\Lambda $.
$\Lambda $.