Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T02:22:23.915Z Has data issue: false hasContentIssue false
  • English
  • Français

JEŚMANOWICZ’ CONJECTURE REVISITED

Part of: Diophantine equations

Published online by Cambridge University Press:  15 February 2013

MIN TANG  and
ZHI-JUAN YANG
MIN TANG*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China
ZHI-JUAN YANG
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 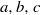$a, b, c$ be relatively prime positive integers such that 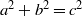${a}^{2} + {b}^{2} = {c}^{2} $. In 1956, Jeśmanowicz conjectured that for any positive integer $n$, the only solution of 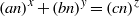$\mathop{(an)}\nolimits ^{x} + \mathop{(bn)}\nolimits ^{y} = \mathop{(cn)}\nolimits ^{z} $ in positive integers is 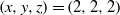$(x, y, z)= (2, 2, 2)$. In this paper, we consider Jeśmanowicz’ conjecture for Pythagorean triples 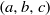$(a, b, c)$ if 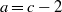$a= c- 2$ and $c$ is a Fermat prime. For example, we show that Jeśmanowicz’ conjecture is true for 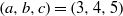$(a, b, c)= (3, 4, 5)$, 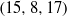$(15, 8, 17)$, 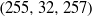$(255, 32, 257)$, 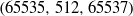$(65535, 512, 65537)$.

Keywords

Jeśmanowicz’ conjectureDiophantine equation

MSC classification

Secondary: 11D61: Exponential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 486 - 491
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Deng, M. J. and Cohen, G. L., ‘On the conjecture of Jeśmanowicz concerning Pythagorean triples’, Bull. Aust. Math. Soc. 57 (1998), 515–524.CrossRefGoogle Scholar
Jeśmanowicz, L., ‘Several remarks on Pythagorean numbers’, Wiad. Mat. 1 (1955/56), 196–202.Google Scholar
Le, M. H., ‘A note on Jeśmanowicz’ conjecture concerning Pythagorean triples’, Bull. Aust. Math. Soc. 59 (1999), 477–480.CrossRefGoogle Scholar
Lu, W. D., ‘On the Pythagorean numbers $4{n}^{2} - 1, 4n$ and $4{n}^{2} + 1$’, Acta Sci. Natur. Univ. Szechuan 2 (1959), 39–42.Google Scholar
Miyazaki, T., ‘Generalizations of classical results on Jeśmanowicz’ conjecture concerning Pythagorean triples’, J. Number Theory 133 (2013), 583–595.CrossRefGoogle Scholar
Miyazaki, T. and Togbé, A., ‘The Diophantine equation $\mathop{(2am- 1)}\nolimits ^{x} + \mathop{(2m)}\nolimits ^{y} = \mathop{(2am+ 1)}\nolimits ^{z} $’, Int. J. Number Theory 8 (2012), 2035–2044.CrossRefGoogle Scholar
Sierpiński, W., ‘On the equation ${3}^{x} + {4}^{y} = {5}^{z} $’, Wiad. Mat. 1 (1955/56), 194–195.Google Scholar
Yang, Z. J. and Tang, M., ‘On the Diophantine equation $\mathop{(8n)}\nolimits ^{x} + \mathop{(15n)}\nolimits ^{y} = \mathop{(17n)}\nolimits ^{z} $’, Bull. Aust. Math. Soc. 86 (2012), 348–352.CrossRefGoogle Scholar