Article contents
ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS
Published online by Cambridge University Press: 08 June 2017
Abstract
Let 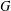 $G$ be a finite solvable group and let
$G$ be a finite solvable group and let 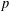 $p$ be a prime. In this note, we prove that
$p$ be a prime. In this note, we prove that 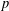 $p$ does not divide
$p$ does not divide 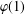 $\unicode[STIX]{x1D711}(1)$ for every irreducible monomial
$\unicode[STIX]{x1D711}(1)$ for every irreducible monomial 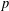 $p$-Brauer character
$p$-Brauer character 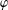 $\unicode[STIX]{x1D711}$ of
$\unicode[STIX]{x1D711}$ of 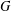 $G$ if and only if
$G$ if and only if 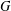 $G$ has a normal Sylow
$G$ has a normal Sylow 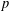 $p$-subgroup.
$p$-subgroup.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 426 - 428
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the China Scholarship Council, Funds of Henan University of Technology (2014JCYJ14, 2016JJSB074, 26510009), Project of Department of Education of Henan Province (17A110004), Projects of Zheng-zhou Municipal Bureau of Science and Technology (20150249, 20140970) and the NSFC (11571129).
References
- 3
- Cited by


