Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T20:14:56.148Z Has data issue: false hasContentIssue false
  • English
  • Français

ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS II

Part of: Representation theory of groups

Published online by Cambridge University Press:  04 October 2017

XIAOYOU CHEN  and
MARK L. LEWIS Open the ORCID record for MARK L. LEWIS [Opens in a new window]
XIAOYOU CHEN
Affiliation:
College of Science, Henan University of Technology, Zhengzhou 450001, China email [email protected]
MARK L. LEWIS*
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 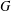$G$ be a finite solvable group and let 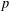$p$ be a prime. We prove that the intersection of the kernels of irreducible monomial 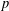$p$-Brauer characters of 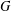$G$ with degrees divisible by 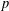$p$ is 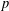$p$-closed.

Keywords

solvable groupItô’s theoremmonomial p-Brauer character

MSC classification

Primary: 20C20: Modular representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 215 - 217
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is supported by the China Scholarship Council, Funds of Henan University of Technology (2014JCYJ14, 2016JJSB074 and 26510009), Project of Department of Education of Henan Province (17A110004), Projects of Zheng-zhou Municipal Bureau of Science and Technology (20150249 and 20140970) and the NSFC (11571129).

References

Chen, X. and Lewis, M., ‘Itô’s theorem and monomial Brauer characters’, Bull. Aust. Math. Soc., doi:10.1017/S0004972717000399.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups (Cambridge University Press, Cambridge, 1993).Google Scholar
Navarro, G., Characters and Blocks of Finite Groups (Cambridge University Press, Cambridge, 1998).Google Scholar
Pang, L. and Lu, J., ‘Finite groups and degrees of irreducible monomial characters’, J. Algebra Appl. 15 (2016), 1650073 (4 pp).Google Scholar
Pang, L. and Lu, J., ‘Finite groups and degrees of irreducible monomial characters II’, J. Algebra Appl. 15 (2017), 1750231 (5 pp).Google Scholar