No CrossRef data available.
Published online by Cambridge University Press: 23 September 2024
Let V be a finite dimensional vector space over the field with p elements, where p is a prime number. Given arbitrary 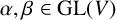 $\alpha ,\beta \in \mathrm {GL}(V)$, we consider the semidirect products
$\alpha ,\beta \in \mathrm {GL}(V)$, we consider the semidirect products 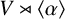 $V\rtimes \langle \alpha \rangle $ and
$V\rtimes \langle \alpha \rangle $ and 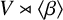 $V\rtimes \langle \beta \rangle $, and show that if
$V\rtimes \langle \beta \rangle $, and show that if 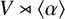 $V\rtimes \langle \alpha \rangle $ and
$V\rtimes \langle \alpha \rangle $ and  $V\rtimes \langle \beta \rangle $ are isomorphic, then
$V\rtimes \langle \beta \rangle $ are isomorphic, then 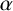 $\alpha $ must be similar to a power of
$\alpha $ must be similar to a power of  $\beta $ that generates the same subgroup as
$\beta $ that generates the same subgroup as 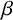 $\beta $; that is, if H and K are cyclic subgroups of
$\beta $; that is, if H and K are cyclic subgroups of  $\mathrm {GL}(V)$ such that
$\mathrm {GL}(V)$ such that 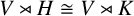 $V\rtimes H\cong V\rtimes K$, then H and K must be conjugate subgroups of
$V\rtimes H\cong V\rtimes K$, then H and K must be conjugate subgroups of 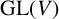 $\mathrm {GL}(V)$. If we remove the cyclic condition, there exist examples of nonisomorphic, let alone nonconjugate, subgroups H and K of
$\mathrm {GL}(V)$. If we remove the cyclic condition, there exist examples of nonisomorphic, let alone nonconjugate, subgroups H and K of 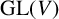 $\mathrm {GL}(V)$ such that
$\mathrm {GL}(V)$ such that 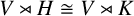 $V\rtimes H\cong V\rtimes K$. Even if we require that noncyclic subgroups H and K of
$V\rtimes H\cong V\rtimes K$. Even if we require that noncyclic subgroups H and K of 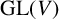 $\mathrm {GL}(V)$ be abelian, we may still have
$\mathrm {GL}(V)$ be abelian, we may still have 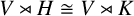 $V\rtimes H\cong V\rtimes K$ with H and K nonconjugate in
$V\rtimes H\cong V\rtimes K$ with H and K nonconjugate in 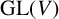 $\mathrm {GL}(V)$, but in this case, H and K must at least be isomorphic. If we replace V by a free module U over
$\mathrm {GL}(V)$, but in this case, H and K must at least be isomorphic. If we replace V by a free module U over 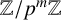 ${\mathbb {Z}}/p^m{\mathbb {Z}}$ of finite rank, with
${\mathbb {Z}}/p^m{\mathbb {Z}}$ of finite rank, with 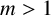 $m>1$, it may happen that
$m>1$, it may happen that 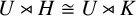 $U\rtimes H\cong U\rtimes K$ for nonconjugate cyclic subgroups of
$U\rtimes H\cong U\rtimes K$ for nonconjugate cyclic subgroups of 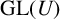 $\mathrm {GL}(U)$. If we completely abandon our requirements on V, a sufficient criterion is given for a finite group G to admit nonconjugate cyclic subgroups H and K of
$\mathrm {GL}(U)$. If we completely abandon our requirements on V, a sufficient criterion is given for a finite group G to admit nonconjugate cyclic subgroups H and K of 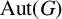 $\mathrm {Aut}(G)$ such that
$\mathrm {Aut}(G)$ such that 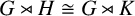 $G\rtimes H\cong G\rtimes K$. This criterion is satisfied by many groups.
$G\rtimes H\cong G\rtimes K$. This criterion is satisfied by many groups.
The third author was supported in part by an NSERC discovery grant.