Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-20T05:29:32.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Ishikawa and Mann iteration methods for nonlinear strongly accretive mappings

Published online by Cambridge University Press:  17 April 2009

M.O. Osilike
M.O. Osilike
Affiliation:
Department of Mathematics, University of Nigeria, Nsukka Nigeria
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a real Banach space with a uniformly convex dual, X*, and let C be a nonempty closed convex and bounded subset of X. Let T: C → C be a strongly accretive and a continuous mapping. For any f ∈ C, let S: C → C be defined by Sx = f + x – Tx for each x ∈ C. Then, the iteration process xo ∈ C,

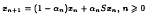
under suitable conditions on the real sequence 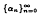converges strongly to a solution of the equation Tx = f in C. Furthermore, if T is strongly accretive and Lipschitz with Lipschitz constant L ≥ 1 then the iteration process x0 ∈ C,

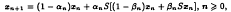
under suitable conditions on the real sequences 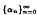and 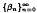converges strongly to a solution of the equation Tx = f in C. Explicit error estimates are obtained.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 46 , Issue 3 , December 1992 , pp. 413 - 424
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Bogin, J., ‘On strict pseudo-contractions and a fixed point theorem’, in Technion Preprint Series No. MT–219 (Herifer, Israel, 1974).Google Scholar
[2]Browder, F.E., ‘Nonlinear mappings of nonexpansive and accretive type in Banach spaces’, Bull. Amer. Math. Soc. 73 (1967), 875–882.CrossRefGoogle Scholar
[3]Browder, F.E., ‘The solvability of nonlinear functional equations’, Duke Math. J. 30 (1963), 557–566.CrossRefGoogle Scholar
[4]Browder, F.E., ‘Nonlinear equation of evolution and nonlinear accretive operators in Banach spaces’, Bull. Amer. Math. Soc. 73 (1967), 470–475.CrossRefGoogle Scholar
[5]Browder, F.E., ‘Nonlinear monotone and accretive operators in Banach spaces’, Proc. Nat. Acad. Sci. U.S.A. 61 (1968), 388–393.CrossRefGoogle ScholarPubMed
[6]Browder, F.E., ‘Nonlinear operators and nonlinear equations of evolution in Banach spaces’, Proc. Sympos. Pure Math. 18 (1976).CrossRefGoogle Scholar
[7]Caristi, J., ‘Fixed point theorems for mappings satisfying inwardness conditions’, Trans. Amer. Math. Soc. 215 (1976), 241–251.CrossRefGoogle Scholar
[8]Chidume, C.E., ‘An approximation method for monotone Lipschitzian operators in Hilbert space’, J. Austral. Math. Soc. (Series A) 41 (1986), 59–63.CrossRefGoogle Scholar
[9]Chidume, C.E., ‘Iterative solution of nonlinear equations of the monotone and dissipative types’, Appl. Anal. 33 (1989), 79–86.CrossRefGoogle Scholar
[10]Chidume, C.E., ‘Fixed point iterations for certain classes of nonlinear mappings, II’, J. Nigerian Math. Soc. 8 (1989), 11–23.Google Scholar
[11]Chidume, C.E., ‘Iterative solution of nonlinear equations of the monotone type in Banach spaces’, Bull. Austral. Math. Soc. 42 (1990), 21–31.CrossRefGoogle Scholar
[12]Chidume, C.E., ‘An iterative process for nonlinear Lipschitzian strongly accretive mappings in Lp spaces’, J. Math. Anal. Appl. 151 (1990), 453–461.CrossRefGoogle Scholar
[13]Deimling, K., ‘Zeros of accretive operators’, Manuscripta Math. 13 (1974), 365–374.CrossRefGoogle Scholar
[14]Dotson, W.G., ‘An iterative process for nonlinear monotonic nonexpansive operators in Hilbert space’, Math. Comp. 32 (1978), 223–225.CrossRefGoogle Scholar
[15]Ishikawa, S., ‘Fixed points by a new iteration method’, Proc. Amer. Math. Soc. 149 (1974), 147–150.CrossRefGoogle Scholar
[16]Kato, T., ‘Nonlinear semigroups and evolution equations’, J. Math. Soc. Japan 18/19 (1967), 508–520.Google Scholar
[17]Kirk, W.A., ‘A fixed point theorem for mappings which do not increase distance’, Amer. Math. Monthly 72 (1965), 1004–1006.CrossRefGoogle Scholar
[18]Mann, W.R., ‘Mean value methods in iteration’, Proc. Amer. Math. Soc. 4 (1953), 506–510.CrossRefGoogle Scholar
[19]Martin, R.H. Jr, ‘A global existence theorem for autonomous differential equations in Banach spaces’, Proc. Amer. Math. Soc. 26 (1970), 307–314.CrossRefGoogle Scholar
[20]Minty, G.J., ‘Monotone (nonlinear) operators in Hilbert space’, Duke Math. J. 29 (1962), 541–546.CrossRefGoogle Scholar
[21]Morales, C., ‘Surjectivity theorems for multi-valued mappings of accretive type’, Comment. Math. Univ. Carolin. 26 (1985).Google Scholar
[22]Nevanlinna, D. and Reich, S., ‘Strong convergence of contraction semi-groups and of iterative methods for accretive operators in Banach spaces’, Israel J. Math. 32 (1976), 44–58.CrossRefGoogle Scholar
[23]Ray, W.O., ‘An elementary proof of surjectivity for a class of accretive operators’, Proc. Amer. Math. Soc. 75 (1979), 255–258.CrossRefGoogle Scholar
[24]Reich, S., ‘An iterative procedure for constructing zeros of accretive sets in Banach spaces’, Nonlinear Anal. 2 (1978), 85–92.CrossRefGoogle Scholar
[25]Rhoades, B.E., ‘Comments on two fixed point iteration methods’, J. Math. Anal. Appl. 56 (1976).CrossRefGoogle Scholar
[26]Smul'yan, V.L., ‘On the derivation of the norm in a Banach space’, Dokl. Akad. Nauk, SSR 27 (1940), 255–258.Google Scholar
[27]Zarantonello, E.H., ‘Solving functional equations by contractive averaging’, Technical Report, No. 160 (U.S. Army Math. Centre, Madison Wisconsin 1960).Google Scholar