Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T14:05:13.646Z Has data issue: false hasContentIssue false
  • English
  • Français

INVERSE LIMITS IN THE CATEGORY OF COMPACT HAUSDORFF SPACES AND UPPER SEMICONTINUOUS FUNCTIONS

Part of: Maps and general types of spaces defined by maps Basic constructions

Published online by Cambridge University Press:  22 March 2013

IZTOK BANIČ  and
TINA SOVIČ
IZTOK BANIČ*
Affiliation:
Faculty of Natural Sciences and Mathematics, University of Maribor, Koroška 160, Maribor 2000, Slovenia Institute of Mathematics, Physics and Mechanics, Jadranska 19, Ljubljana 1000, Slovenia
TINA SOVIČ
Affiliation:
Faculty of Civil Engineering, University of Maribor, Smetanova 17, Maribor 2000, Slovenia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate inverse limits in the category 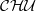$ \mathcal{CHU} $ of compact Hausdorff spaces with upper semicontinuous functions. We introduce the notion of weak inverse limits in this category and show that the inverse limits with upper semicontinuous set-valued bonding functions (as they were defined by Ingram and Mahavier [‘Inverse limits of upper semi-continuous set valued functions’, Houston J. Math.  32 (2006), 119–130]) together with the projections are not necessarily inverse limits in 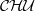$ \mathcal{CHU} $ but they are always weak inverse limits in this category. This is a realisation of our categorical approach to solving a problem stated by Ingram [An Introduction to Inverse Limits with Set-Valued Functions (Springer, New York, 2012)].

Keywords

upper semi-continuous functionsinverse limitsweak inverse limits

MSC classification

Secondary: 54C60: Set-valued maps 54B30: Categorical methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 49 - 59
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Banič, I., ‘On dimension of inverse limits with upper semicontinuous set-valued bonding functions’, Topology Appl. 154 (2007), 2771–2778.CrossRefGoogle Scholar
Banič, I., ‘Inverse limits as limits with respect to the Hausdorff metric’, Bull. Aust. Math. Soc. 75 (2007), 17–22.CrossRefGoogle Scholar
Banič, I., ‘Continua with kernels’, Houston J. Math. 34 (2008), 145–163.Google Scholar
Banič, I., Črepnjak, M., Merhar, M. and Milutinović, U., ‘Limits of inverse limits’, Topology Appl. 157 (2010), 439–450.CrossRefGoogle Scholar
Banič, I., Črepnjak, M., Merhar, M. and Milutinović, U., ‘Paths through inverse limits’, Topology Appl. 158 (2011), 1099–1112.CrossRefGoogle Scholar
Banič, I., Črepnjak, M., Merhar, M. and Milutinović, U., ‘Towards the complete classification of generalized tent maps inverse limits’, Topology Appl. 160 (2013), 63–73.Google Scholar
Banič, I., Črepnjak, M., Merhar, M., Milutinović, U. and Sovič, T., ‘Ważewski’s universal dendrite as an inverse limit with one set-valued bonding function’, Glas. Mat. Ser. III, in press.Google Scholar
Charatonik, W. J. and Roe, R. P., ‘Inverse limits of continua having trivial shape’, Houston J. Math. 38 (2012), 1307–1312.Google Scholar
Cornelius, A. N., ‘Weak crossovers and inverse limits of set-valued functions’, Preprint, 2009.Google Scholar
Illanes, A., ‘A circle is not the generalized inverse limit of a subset of $\mathop{[0, 1] }\nolimits ^{2} $’, Proc. Amer. Math. Soc. 139 (2011), 2987–2993.CrossRefGoogle Scholar
Ingram, W. T., ‘Inverse limits of upper semicontinuous functions that are unions of mappings’, Topology Proc. 34 (2009), 17–26.Google Scholar
Ingram, W. T., ‘Inverse limits with upper semicontinuous bonding functions: problems and some partial solutions’, Topology Proc. 36 (2010), 353–373.Google Scholar
Ingram, W. T., An Introduction to Inverse Limits with Set-valued Functions (Springer, New York, 2012).CrossRefGoogle Scholar
Ingram, W. T. and Mahavier, W. S., ‘Inverse limits of upper semi-continuous set valued functions’, Houston J. Math. 32 (2006), 119–130.Google Scholar
Kennedy, J. A. and Greenwood, S., ‘Pseudoarcs and generalized inverse limits’, Preprint, 2010.Google Scholar
Mahavier, W. S., ‘Inverse limits with subsets of $[0, 1] \times [0, 1] $’, Topology Appl. 141 (2004), 225–231.CrossRefGoogle Scholar
Mardešić, S. and Segal, J., Shape Theory (North-Holland, Amsterdam, 1982).Google Scholar
Nall, V., ‘Inverse limits with set valued functions’, Houston J. Math. 37 (2011), 1323–1332.Google Scholar
Nall, V., ‘Connected inverse limits with set valued functions’, Topology Proc. 40 (2012), 167–177.Google Scholar
Nall, V., ‘Finite graphs that are inverse limits with a set valued function on $[0, 1] $’, Topology Appl. 158 (2011), 1226–1233.Google Scholar
Palaez, A., ‘Generalized inverse limits’, Houston J. Math. 32 (2006), 1107–1119.Google Scholar
Varagona, S., ‘Inverse limits with upper semi-continuous bonding functions and indecomposability’, Houston J. Math. 37 (2011), 1017–1034.Google Scholar