Lattice walk problems in the quarter-plane have been widely studied in recent years. The main objective is to calculate the number of configurations, that is, the number of n-step walks ending at certain points or, alternatively, the generating function of the walks. In combinatorics, physics and probability theory, other properties such as asymptotic behaviour and the algebra of the generating functions are also of interest.
In this thesis we focus on solving quarter-plane lattice walks with interactions via the kernel method. We assign interaction a to the x-axis, b to the y-axis and c to the origin. We denote
![]() $q_{n,k,l,h,u,v}$
as the number of n-step paths that start at point
$q_{n,k,l,h,u,v}$
as the number of n-step paths that start at point
![]() $(0,0)$
and end at point
$(0,0)$
and end at point
![]() $(k,l)$
and which visit vertices on the horizontal boundary (except the origin) h times, vertices on the vertical boundary (except the origin) v times and the origin u times. Then
$(k,l)$
and which visit vertices on the horizontal boundary (except the origin) h times, vertices on the vertical boundary (except the origin) v times and the origin u times. Then
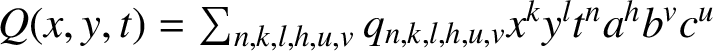 $Q(x,y,t)=\sum _{n,k,l,h,u,v} q_{n,k,l,h,u,v}x^k y^l t^n a^h b^v c^u$
is the generating function of the walk. Our aim is to find whether the interactions will affect the solubility of quarter-plane lattice walk models and the properties of the generating functions
$Q(x,y,t)=\sum _{n,k,l,h,u,v} q_{n,k,l,h,u,v}x^k y^l t^n a^h b^v c^u$
is the generating function of the walk. Our aim is to find whether the interactions will affect the solubility of quarter-plane lattice walk models and the properties of the generating functions
![]() $Q(x,y,t)$
. In particular, we give solutions to all
$Q(x,y,t)$
. In particular, we give solutions to all
![]() $23$
quarter-plane lattice walks associated with finite groups. We solve
$23$
quarter-plane lattice walks associated with finite groups. We solve
![]() $21$
of them explicitly, writing an expression for the generating functions
$21$
of them explicitly, writing an expression for the generating functions
![]() $Q(x,y,t)$
. The other two are only partly solved. We discuss when the generating function
$Q(x,y,t)$
. The other two are only partly solved. We discuss when the generating function
![]() $Q(x,y,t)$
becomes D-algebraic, D-finite and algebraic by the variations of
$Q(x,y,t)$
becomes D-algebraic, D-finite and algebraic by the variations of
![]() $a,b,c$
.
$a,b,c$
.
We also compare the solutions obtained by the kernel method and the solutions obtained by an analytic method based on homomorphisms on a Riemann surface. We combine the solutions in another form with the solution of the kernel method and prove the properties of the generating function
![]() $Q(x,y,t)$
. We observe that the solution obtained using the kernel method and other analytic methods are consistent with one another.
$Q(x,y,t)$
. We observe that the solution obtained using the kernel method and other analytic methods are consistent with one another.
Some of this research has appeared in [Reference Beaton, Owczarek and Xu1, Reference Beaton, Owczarek, Xu, Bostan and Raschel2].



