Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T06:49:30.397Z Has data issue: false hasContentIssue false
  • English
  • Français

Integration Operator Acting on Hardy and Weighted Bergman Spaces

Published online by Cambridge University Press:  17 April 2009

Jouni Rättyä
Jouni Rättyä
Affiliation:
University of Joensuu, Department of Mathematics, P.O. Box 111, 80101 Joensuu, Finland, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

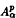Questions related to the operator Jg(f)(z):= ∫xof (ζ)g′(ζ) dζ, induced by an analytic function g in the unit disc, are studied. It is shown that a function G is the derivative of a function in the Hardy space Hp if and only if it is of the form G = Fψ′ where F ∈ Hq, ψ ∈ H3 and 1/s = 1/p − 1/q. Moreover, a complete characterisation of when Jg is bounded or compact from one weighted Bergman space into another is established, and an asymptotic formula for the essential norm of Jg, the distance from compact operators in the operator norm, is given. As an immediate consequence it is obtained that if p < 2 + α and α > −1, then any primitive of 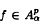belongs to 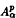where q = ((2 + α) p)/(2 + α − p). For α = −1 this is a sharp result by Hardy and Littlewood on primitives of functions in Hardy space 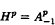, 0 < p < 1.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 75 , Issue 3 , June 2007 , pp. 431 - 446
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Aleman, A. and Cima, J.A., ‘An integral operator on Hp and Hardy's inequality’, J. Anal. Math. 85 (2001), 157–176.CrossRefGoogle Scholar
[2]Aleman, A. and Siskakis, A.G., ‘An integral operator on Hp’ Complex Variables Theory Appl. 28 (1995), 149–158.Google Scholar
[3]Aleman, A. and Siskakis, A.G., ‘Integration operators on Bergman spaces’, Indiana Univ. Math. J. 46 (1997), 337–356.CrossRefGoogle Scholar
[4]Aulaskari, R., Stegenga, D., and Xiao, J., ‘Some subclasses of BMOA and their characterization in terms of Carleson measures’, Rocky Mountain J. Math. 26 (1996), 485–506.CrossRefGoogle Scholar
[5]Baernstein, A. II, ‘Analytic functions of bounded mean oscillation’, in in Aspects of Contemporary Complex Analysis, (Brannan, D. and Clunie, J., Editors) (Academic Press, London, New York, 1980), pp. 3–36.Google Scholar
[6]Carleson, L., ‘An interpolation problem for bounded analytic functions’, Amer. J. Math. 80 (1958), 921–930.CrossRefGoogle Scholar
[7]Carleson, L., ‘Interpolations by bounded analytic functions and the corona problem’, Ann. of Math. (2) 76 (1962), 547–559.CrossRefGoogle Scholar
[8]Cima, J.A. and Schober, G., ‘Analytic functions with bounded mean oscillation and logarithms of Hp functions’, Math. Z. 151 (1976), 295–300.CrossRefGoogle Scholar
[9]Cohn, W.S., ‘A factorization theorem for the derivative of a function in Hp’, Proc. Amer. Math. Soc. 127 (1999), 509–517.CrossRefGoogle Scholar
[10]Cowen, C.C. and MacCluer, B.D., Composition operators on spaces of analytic functions, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1995).Google Scholar
[11]Duren, P., ‘Extension of a Theorem of Carleson’, Bull. Amer. Math. Soc. 75 (1969), 143–146.CrossRefGoogle Scholar
[12]Duren, P., Theory of Hp spaces (Academic Press, New York, London, 1970).Google Scholar
[13]Flett, T.M., ‘The dual of an inequality of Hardy and Littlewood and some related inequalitites’, J. Math. Anal. Appl. 38 (1972), 746–765.CrossRefGoogle Scholar
[14]Garnett, J., Bounded analytic functions (Academic Press, New York, 1981).Google Scholar
[15]Hardy, G.H. and Littlewood, J.E., ‘Some more theorems concerning Fourier series and Fourier power series’, Duke Math. J. 2 (1936), 354–382.CrossRefGoogle Scholar
[16]Jarchow, H., ‘Embeddings induced by planar Carleson measures’,in Function spaces and operator theory, Proceedings of the Summer School held at the University of Joensuu,Joensuu,May 19–23, 2003, (Taskinen, Jari, Editor), University of Joensuu, Department of Mathematics. Report Series, 8 (University of Joensuu, Joensuu, 2005).Google Scholar
[17]Luecking, D.H., ‘A new proof of an inequality of Littlewood and Paley’, Proc. Amer. Math. Soc. 103 (1988), 887–893.CrossRefGoogle Scholar
[18]Luecking, D.H., ‘Embedding theorems for spaces of analytic functions via Khinchine's inequality’, Michigan Math. J. 40 (1993), 333–358.CrossRefGoogle Scholar
[19]Pommerenke, Ch., Univalent functions, Studia Mathematica/Mathematische Lehrbücher, Band XXV, (With a chapter on quadratic differentials by Gerd Jensen (Vandenhoeck and Ruprecht, Göttingen, 1975).Google Scholar
[20]Pommerenke, Ch., ‘Schlichte Funktionen und analytische Funktionen von beschränkter mittlerer Oszillation’, (German), Comment. Math. Helv. 52 (1977), 591–602.CrossRefGoogle Scholar
[21]Shapiro, J.H., ‘The essential norm of a composition operator’, Ann. Math. 125 (1987), 375–404.CrossRefGoogle Scholar
[22]Siskakis, A.G., Studies on composition operators (Laramie, WY, 1996), in, Contemp. Math. 213 (Amer. Math. Soc., Providence, RI, 1998), pp. 229–252.CrossRefGoogle Scholar
[23]Siskakis, A.G. and Zhao, R., ‘A Volterra type operator on spaces of analytic functions’, in Function spaces (Edwardsville, IL, 1998), Contemp. Math. 232 (Amer. Math. Soc., Providence, RI, 1999), pp. 299–311.CrossRefGoogle Scholar
[24]Vinogradov, S.A., ‘Multiplication and division in the space of analytic functions with an area-integrable derivative, and in some related spaces’, Issled. po Linein. Oper. i Teor. Funktsii. 23 (1995), 45–77. Translation in J. Math. Sci. (New York) 87 (1997), 3806–3827.Google Scholar
[25]Vukotić, D., ‘A sharp estimate for functions in ℂn’, Proc. Amer. Math. Soc. 117 (1993), 753–756.Google Scholar
[26]Wu, Z., ‘Carleson measures and multipliers for Dirichlet spaces’, J. Func. Anal. 169 (1999), 148–163.CrossRefGoogle Scholar
[27]Yamashita, S., ‘Gap series and α-Bloch functions’, Yokohama Math. J. 28 (1980), 31–36.Google Scholar
[28]Zhao, R., ‘Pointwise multipliers from weighted Bergman spaces and Hardy spaves on weighted Bergman spaces’, Ann. Acad. Sci. Fenn. Math. 29 (2004), 139–150.Google Scholar
[29]Zhu, K., Operator theory in function spaces (Marcel Dekker, New York, 1990).Google Scholar
[30]Zhu, K., ‘Translating inequalities between Hardy and Bergman spaces’, Amer. Math. Montly 111 (2004), 520–525.CrossRefGoogle Scholar
[31]Zygmund, A., Trigonometric series (Cambridge University Press, London, 1959).Google Scholar