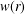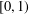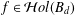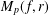Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Doubtsov, Evgueni
2019.
Integration and Differentiation in Hardy Growth Spaces.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 4,
p.
1883.
Bucyanayandi, Emmanuel
Ergül, Muhammed Said
and
Kocabaş, İbrahim
2023.
A Comparison of The Performances of Conventional and Low Salinity Water Alternating Gas Injection for Displacement of Oil.
Scientific Research Communications,
Vol. 3,
Issue. 1,
p.
1.