Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T03:20:01.807Z Has data issue: false hasContentIssue false
  • English
  • Français

INJECTIVE TRANSFORMATIONS WITH EQUAL GAP AND DEFECT

Part of: Semigroups

Published online by Cambridge University Press:  13 March 2009

JINTANA SANWONG  and
R. P. SULLIVAN
JINTANA SANWONG
Affiliation:
Department of Mathematics, Chiangmai University, Chiangmai, 50200, Thailand
R. P. SULLIVAN*
Affiliation:
School of Mathematics and Statistics, University of Western Australia, Nedlands 6009, Australia (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that X is an infinite set and I(X) is the symmetric inverse semigroup defined on X. If α∈I(X), we let dom α and ran α denote the domain and range of α, respectively, and we say that g(α)=|X/dom α| and d(α)=|X/ran α| is the ‘gap’ and the ‘defect’ of α, respectively. In this paper, we study algebraic properties of the semigroup 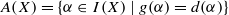. For example, we describe Green’s relations and ideals in A(X), and determine all maximal subsemigroups of A(X) when X is uncountable.

Keywords

factorizable inverse semigroupgapdefectGreen’s relationsidealsmaximal subsemigroup

MSC classification

Secondary: 20M20: Semigroups of transformations, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 79 , Issue 2 , April 2009 , pp. 327 - 336
Copyright
Copyright © Australian Mathematical Society 2009

References

[1] Bairamov, R. A., ‘On the problem of completeness in a symmetric semigroup of finite degree’, Diskret. Anal. 8 (1966), 3–26 (in Russian).Google Scholar
[2] Chen, S. Y. and Hsieh, S. C., ‘Factorizable inverse semigroups’, Semigroup Forum 8 (1974), 283–297.CrossRefGoogle Scholar
[3] Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, Mathematical Surveys, No. 7, Parts 1 and 2 (American Mathematical Society, Providence, RI, 1961 and 1967).Google Scholar
[4] Hotzel, E., ‘Maximality properties of some subsemigroups of Baer–Levi semigroups’, Semigroup Forum 51 (1995), 153–190.CrossRefGoogle Scholar
[5] Howie, J. M., Fundamentals of Semigroup Theory, London Mathematics Society Monographs (NS), 12 (Clarendon Press, Oxford, 1995).CrossRefGoogle Scholar
[6] Howie, J. M., ‘A congruence-free inverse semigroup associated with a pair of infinite cardinals’, J. Aust. Math. Soc. 31A (1981), 337–342.Google Scholar
[7] Jampachon, P., Saichalee, M. and Sullivan, R. P., ‘Locally factorisable transformation semigroups’, Southeast Asian Bull. Math. 25 (2001), 233–244.Google Scholar
[8] Levi, I. and Wood, G. R., ‘On maximal subsemigroups of Baer–Levi semigroups’, Semigroup Forum 30(1) (1984), 99–102.CrossRefGoogle Scholar
[9] Reynolds, M. A. and Sullivan, R. P., ‘The ideal structure of idempotent-generated transformation semigroups’, Proc. Edinburgh Math. Soc. 28(3) (1985), 319–331.CrossRefGoogle Scholar
[10] Sullivan, R. P., ‘Semigroups generated by nilpotent transformations’, J. Algebra 110(2) (1987), 324–343.CrossRefGoogle Scholar
[11] Yang, H. B. and Yang, X. L., ‘Maximal subsemigroups of finite transformation semigroups K(n,r)’, Acta Math. Sin. (Engl. Ser.) 20(3) (2004), 475–482.Google Scholar
[12] Yang, X., ‘Maximal subsemigroups of the finite singular transformation semigroup’, Comm. Algebra 29(3) (2001), 1175–1182.Google Scholar