Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fu, Xian-Hui
and
Ding, Nan-Qing
2010.
TORSION THEORIES AND ESSENTIAL FLAT ENVELOPES.
Taiwanese Journal of Mathematics,
Vol. 14,
Issue. 4,
Abdioĝlu, Cihad
Khashyarmanesh*, Kazem
and
Tamer Koşan, M.
2011.
On the support of general local cohomology modules and filter regular sequences.
Quaestiones Mathematicae,
Vol. 34,
Issue. 4,
p.
479.
Khashyarmanesh, K.
and
Khosh-Ahang, F.
2012.
Local Cohomology Modules, Serre Subcategories and Derived Functors of Torsion Functors.
Algebra Colloquium,
Vol. 19,
Issue. spec01,
p.
1187.
Selvaraj, C.
and
Umamaheswaran, A.
2016.
Stability of Gorenstein X-flat modules.
Lobachevskii Journal of Mathematics,
Vol. 37,
Issue. 2,
p.
193.
Umamaheswaran, Arunachalam
Udhayakumar, Ramalingam
Selvaraj, Chelliah
Tamilvanan, Kandhasamy
Kabeto, Masho Jima
and
Meyer, Ralf
2022.
Existence of Covers and Envelopes of a Left Orthogonal Class and Its Right Orthogonal Class of Modules.
Journal of Mathematics,
Vol. 2022,
Issue. 1,


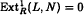 for all
for all 