Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Thompson, R.C.
1975.
Singular value inequalities for matrix sums and minors.
Linear Algebra and its Applications,
Vol. 11,
Issue. 3,
p.
251.
1979.
Inequalities - Theory of Majorization and Its Applications.
Vol. 143,
Issue. ,
p.
531.
Sharma, C.S.
1985.
A simple proof of the inequality of Thompson and Therianos concerning sums of eigenvalues of a hermitian matrix.
Physics Letters A,
Vol. 111,
Issue. 6,
p.
261.
Kolotilina, L.Yu.
1998.
Eigenvalue bounds and inequalities using vector aggregation of matrices.
Linear Algebra and its Applications,
Vol. 271,
Issue. 1-3,
p.
139.
Li, Chi-Kwong
and
Mathias, Roy
2002.
Inequalities on Singular Values of Block Triangular Matrices.
SIAM Journal on Matrix Analysis and Applications,
Vol. 24,
Issue. 1,
p.
126.
Schreier, P.J.
Scharf, L.L.
and
Mullis, C.T.
2003.
A unified approach to performance comparisons between linear and widely linear processing.
p.
114.
Schreier, P.J.
Scharf, L.L.
and
Mullis, C.T.
2005.
Detection and Estimation of Improper Complex Random Signals.
IEEE Transactions on Information Theory,
Vol. 51,
Issue. 1,
p.
306.
Kolotilina, L. Yu.
2018.
An Upper Bound for the Largest Eigenvalue of a Positive Semidefinite Block Banded Matrix.
Journal of Mathematical Sciences,
Vol. 232,
Issue. 6,
p.
917.
Mordant, Gilles
and
Segers, Johan
2022.
Measuring dependence between random vectors via optimal transport.
Journal of Multivariate Analysis,
Vol. 189,
Issue. ,
p.
104912.
De Keyser, Steven
and
Gijbels, Irène
2025.
High-dimensional copula-based Wasserstein dependence.
Computational Statistics & Data Analysis,
Vol. 204,
Issue. ,
p.
108096.


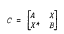 be a hermitian matrix in partitioned form. Let the eigenvalues of
be a hermitian matrix in partitioned form. Let the eigenvalues of