Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T02:15:15.040Z Has data issue: false hasContentIssue false
  • English
  • Français

INDECOMPOSABLE REPRESENTATIONS OF THE EUCLIDEAN ALGEBRA 𝔢(3) FROM IRREDUCIBLE REPRESENTATIONS OF

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  01 April 2011

ANDREW DOUGLAS  and
JOE REPKA
ANDREW DOUGLAS*
Affiliation:
Department of Mathematics, New York City College of Technology, City University of New York, 300 Jay Street, Brooklyn, NY 11201, USA (email: [email protected])
JOE REPKA
Affiliation:
Department of Mathematics, University of Toronto, 40 St. George Street, Toronto, ON, Canada M5S 2E4 (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

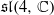
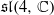The Euclidean group E(3) is the noncompact, semidirect product group E(3)≅ℝ3⋊SO(3). It is the Lie group of orientation-preserving isometries of three-dimensional Euclidean space. The Euclidean algebra 𝔢(3) is the complexification of the Lie algebra of E(3). We embed the Euclidean algebra 𝔢(3) into the simple Lie algebra and show that the irreducible representations V (m,0,0) and V (0,0,m) of 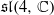are 𝔢(3)-indecomposable, thus creating a new class of indecomposable 𝔢(3) -modules. We then show that V (0,m,0) may decompose.

Keywords

Euclidean algebraindecomposable representationsLie algebra embedding

MSC classification

Secondary: 17B10: Representations, algebraic theory (weights)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 83 , Issue 3 , June 2011 , pp. 439 - 449
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

Footnotes

The work of A.D. is partially supported by the Professional Staff Congress/City University of New York (PSC/CUNY). The work of J.R. is partially supported by the Natural Sciences and Engineering Research Council (NSERC).

References

[1]Casati, P., ‘Irreducible SLn+1-representations remain indecomposable restricted to some abelian subalgebras’, J. Lie Theory 20(2) (2010), 393–407.Google Scholar
[2]Casati, P., Minniti, S. and Salari, V., ‘Indecomposable representations of the Diamond Lie algebra’, J. Math. Phys. 51 (2010), 033515.CrossRefGoogle Scholar
[3]Douglas, A. and Premat, A., ‘A class of nonunitary representations of the Euclidean algebra 𝔢(2)’, Comm. Algebra 35(5) (2007), 1433–1448.CrossRefGoogle Scholar
[4] ‘GAP – Groups, Algorithms, Programming’, Version 4.2, 2000, http://www-gap.dcs.st-and.ac.uk/∼gap.Google Scholar
[5]Hall, B. C., Lie Groups, Lie Algebras, and Representations (Springer, New York, 2003).CrossRefGoogle Scholar
[6]Humphreys, J. E., Introduction to Lie Algebras and Representation Theory (Springer, New York, 1972).CrossRefGoogle Scholar
[7]Littelmann, P., ‘An algorithm to compute bases and representation matrices for SLn+1-representations’, J. Pure Appl. Algebra 117/ 118 (1997), 447–468.CrossRefGoogle Scholar