Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-12T00:50:48.762Z Has data issue: false hasContentIssue false
  • English
  • Français

Homomorphisms of distributive p-algebras with countably many minimal prime ideals

Published online by Cambridge University Press:  17 April 2009

M. E. Adams ,
V. Koubek  and
J. Sichler
M. E. Adams
Affiliation:
Department of Mathematics, State University of New York, New Paltz, NY 12561, U.S.A.
V. Koubek
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, Manitoba, Canada R3T 2N2
J. Sichler
Affiliation:
MFF KU, Malostranské nám. 25, 118 00 Praha 1, Czechoslovakia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

According to a result of Lee, varieties of pseudocomplemented distributive lattices form an ω+1 chain 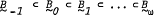in which 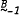is the trivial variety and 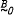is the variety of Boolean algebras. In the present paper it is shown that the variety 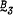contains an almost universal subcategory B in which the members of Hom(B,B') associated with minimal prime ideals of B form a countably infinite set for any B,B' ∈ B. In particular, B3contains arbitrarily large algebras whose nontrivial endomorphisms form the countably infinite right zero semigroup. Our earlier results concerning categorical properties of varieties of pseudocomplemented distributive lattices show that no further reduction of the right zero count is possible.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 35 , Issue 3 , June 1987 , pp. 427 - 439
Copyright
Copyright © Australian Mathematical Society 1987

References

[1]Adams, M. E., Koubek, V. and Sichler, J., “Homomorphisms and endomorphisms in varieties of pseudocomplemented distributive lattices (with applications to Heyting algebras)”, Trans. Amer. Math. Soc. 285 (1984), 57–79.CrossRefGoogle Scholar
[2]Adams, M. E., Koubek, V. and Sichler, J., “Pseudocomplemented distributive lattices with small endomorphism monoids”, Bull. Austral. Math. Soc. 28 (1983), 305–318.CrossRefGoogle Scholar
[3]Balbes, R. and Dwinger, Ph., Distributive Lattices, (University of Missouri Press, Columbia, Missouri, 1974).Google Scholar
[4]Davey, B. A. and Duffus, D., “Exponentiation and duality”, in Ordered Sets, (Reidel, Dordrecht, 1982), 43–95.CrossRefGoogle Scholar
[5]Koubek, V., “Infinite image homomorphisms of distributive bounded lattices”, in Universal Algebra, (Colloq. Math. Soc. János Bolyai 43, North-Holland, Amsterdam, 1985).Google Scholar
[6]Lee, K. B. “Equational classes of distributive pseudocomplemented lattices”, Canada J. Math. 22 (1970), 881–891.CrossRefGoogle Scholar
[7]Pigozzi, D. and Sichler, J., “Homomorphisms of partial and of complete Steiner triple systems and quasigroups”, in Universal Algebra and Lattice Theory, (Lecture Notes in Mathematics 1149, Springer-Verlag, Berlin, 1985, 224–237).CrossRefGoogle Scholar
[8]Priestley, H. A., “Representation of distributive lattices by means of ordered Stone spaces”, Bull. London Math. Soc. 2 (1970), 186–190.CrossRefGoogle Scholar
[9]Priestley, H. A., “The construction of spaces dual to pseudo-complemented distributive lattices”, Quart. J. Math. Oxford Ser. (2) 26 (1975), 215–228.CrossRefGoogle Scholar
[10]Priestley, H. A., “Ordered sets and duality for distributive lattices”, Ann. Discrete Math. 23 (1984), 39–60.Google Scholar
[11]Pultr, A. and Trnková, V., Combinatorial, algebraic and topological representations of groups, semigroups and categories, (North-Holland, Amsterdam, 1980).Google Scholar
[12]Ribenboim, P., “Characterization of the sup-complement in a distributive lattice with last element”, Summa Brasil Math. 2 (1949), 43–49.Google Scholar