1. Introduction
Several deep arithmetic questions are known about polynomials with integer coefficients. One of them raised by Lehmer in the 1930s asks, for a monic irreducible polynomial
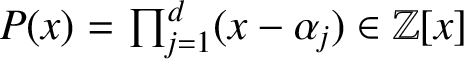 $P(x)=\prod _{j=1}^d(x-\alpha _j)\in \mathbb Z[x]$
, whether the quantity
$P(x)=\prod _{j=1}^d(x-\alpha _j)\in \mathbb Z[x]$
, whether the quantity
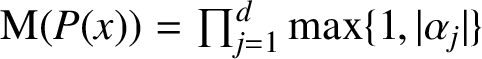 ${\mathrm M}(P(x))=\prod _{j=1}^d\max \{1,|\alpha _j|\}$
can be made arbitrarily close to but greater than 1. The characteristic
${\mathrm M}(P(x))=\prod _{j=1}^d\max \{1,|\alpha _j|\}$
can be made arbitrarily close to but greater than 1. The characteristic
![]() ${\mathrm M}(P(x))$
is known as the Mahler measure [Reference Brunault and Zudilin1]; in spite of the name coined after Mahler’s work in the 1960s, many results about it are rather classical. One of them, due to Kronecker, says that
${\mathrm M}(P(x))$
is known as the Mahler measure [Reference Brunault and Zudilin1]; in spite of the name coined after Mahler’s work in the 1960s, many results about it are rather classical. One of them, due to Kronecker, says that
![]() ${\mathrm M}(P(x))=1$
if and only if
${\mathrm M}(P(x))=1$
if and only if
![]() $P(x)=x$
or the polynomial is cyclotomic, that is, all its zeros are roots of unity.
$P(x)=x$
or the polynomial is cyclotomic, that is, all its zeros are roots of unity.
A related question, usually considered as a satellite to Lehmer’s problem, about the so-called house of a nonzero algebraic integer
![]() $\alpha $
defined through its minimal polynomial
$\alpha $
defined through its minimal polynomial
![]() $P(x)\in \mathbb Z[x]$
as
$P(x)\in \mathbb Z[x]$
as
![]() , was posed by Schinzel and Zassenhaus in the 1960s and answered only recently by Dimitrov [Reference Dimitrov2]. He proved that
, was posed by Schinzel and Zassenhaus in the 1960s and answered only recently by Dimitrov [Reference Dimitrov2]. He proved that
![]() for any nonzero algebraic integer
for any nonzero algebraic integer
![]() $\alpha $
which is not a root of unity; the latter option clearly corresponds to
$\alpha $
which is not a root of unity; the latter option clearly corresponds to
![]() .
.
Dimitrov’s ingenious argument transforms the arithmetic problem into an analytic one. In this note we discuss the potential of Dimitrov’s approach to Lehmer’s problem.
2. Principal results
Consider a monic irreducible noncyclotomic polynomial
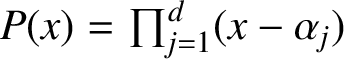 $P(x)=\prod _{j=1}^d(x-\alpha _j)$
in
$P(x)=\prod _{j=1}^d(x-\alpha _j)$
in
![]() $\mathbb Z[x]$
of degree
$\mathbb Z[x]$
of degree
![]() $d>1$
and assume that the polynomial
$d>1$
and assume that the polynomial
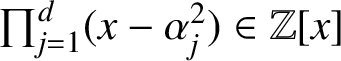 $\prod _{j=1}^d(x-\alpha _j^2)\in \mathbb Z[x]$
is irreducible as well. (Otherwise the Mahler measure of
$\prod _{j=1}^d(x-\alpha _j^2)\in \mathbb Z[x]$
is irreducible as well. (Otherwise the Mahler measure of
![]() $P(x)$
is bounded from below through the measures of irreducible factors of the latter polynomial.) As in [Reference Dimitrov2], Dimitrov’s cyclotomicity criterion together with Kronecker’s rationality criterion and a theorem of Pólya imply that the hedgehog
$P(x)$
is bounded from below through the measures of irreducible factors of the latter polynomial.) As in [Reference Dimitrov2], Dimitrov’s cyclotomicity criterion together with Kronecker’s rationality criterion and a theorem of Pólya imply that the hedgehog
 $$ \begin{align*}K=K(\beta_1,\dots,\beta_n)=\bigcup_{k=1}^n[0,\beta_j] =\bigcup_{j=1}^d[0,\alpha_j^2]\cup\bigcup_{j=1}^d[0,\alpha_j^4], \end{align*} $$
$$ \begin{align*}K=K(\beta_1,\dots,\beta_n)=\bigcup_{k=1}^n[0,\beta_j] =\bigcup_{j=1}^d[0,\alpha_j^2]\cup\bigcup_{j=1}^d[0,\alpha_j^4], \end{align*} $$
whose spines originate from the origin and end up at
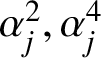 $\alpha _j^2,\alpha _j^4$
for
$\alpha _j^2,\alpha _j^4$
for
![]() $j=1,\dots ,d$
, has (logarithmic) capacity (or transfinite diameter)
$j=1,\dots ,d$
, has (logarithmic) capacity (or transfinite diameter)
![]() $t(K)$
at least 1. Then Dubinin’s theorem [Reference Dubinin3] applies, which claims that
$t(K)$
at least 1. Then Dubinin’s theorem [Reference Dubinin3] applies, which claims that
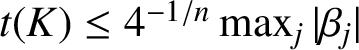 $t(K)\le 4^{-1/n}\max _j|\beta _j|$
(with equality attained if and only if the hedgehog K is rotationally symmetric), and produces the estimate for
$t(K)\le 4^{-1/n}\max _j|\beta _j|$
(with equality attained if and only if the hedgehog K is rotationally symmetric), and produces the estimate for
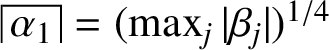 since
since
![]() $n\le 2d$
.
$n\le 2d$
.
When dealing with Lehmer’s problem instead, one becomes interested in estimating the ‘Mahler measure of the hedgehog’, namely the quantity
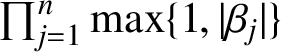 $\prod _{j=1}^n\max \{1,|\beta _j|\}$
, because any nontrivial (bounded away from 1) absolute estimate for it would imply a nontrivial estimate for the Mahler measure of
$\prod _{j=1}^n\max \{1,|\beta _j|\}$
, because any nontrivial (bounded away from 1) absolute estimate for it would imply a nontrivial estimate for the Mahler measure of
![]() $P(x)$
. In this setting, Dubinin’s theorem only implies the estimate
$P(x)$
. In this setting, Dubinin’s theorem only implies the estimate
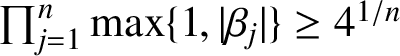 $\prod _{j=1}^n\max \{1,|\beta _j|\}\ge 4^{1/n}$
for a hedgehog of capacity at least 1, which depends on n. The Mahler measure of the rotationally symmetric hedgehog on n spines, which is optimal in Dubinin’s result, is equal to 4 (thus, independent of n), which certainly loses out to the Mahler measure
$\prod _{j=1}^n\max \{1,|\beta _j|\}\ge 4^{1/n}$
for a hedgehog of capacity at least 1, which depends on n. The Mahler measure of the rotationally symmetric hedgehog on n spines, which is optimal in Dubinin’s result, is equal to 4 (thus, independent of n), which certainly loses out to the Mahler measure
![]() $1.91445008\dots $
of the ‘Lehmer hedgehog’ attached to the polynomial
$1.91445008\dots $
of the ‘Lehmer hedgehog’ attached to the polynomial
![]() $x^{10}+x^9-x^7-x^6-x^5-x^4-x^3+x+1$
but also to the measure
$x^{10}+x^9-x^7-x^6-x^5-x^4-x^3+x+1$
but also to the measure
![]() $3.07959562\dots $
of the hedgehog constructed on Smyth’s polynomial
$3.07959562\dots $
of the hedgehog constructed on Smyth’s polynomial
![]() $x^3-x-1$
. The following question arises in a natural way.
$x^3-x-1$
. The following question arises in a natural way.
Question 1. What is the minimum of
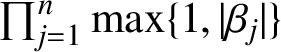 $\prod _{j=1}^n\max \{1,|\beta _j|\}$
taken over all hedgehogs
$\prod _{j=1}^n\max \{1,|\beta _j|\}$
taken over all hedgehogs
![]() $K=K(\beta _1,\dots ,\beta _n)$
of capacity at least
$K=K(\beta _1,\dots ,\beta _n)$
of capacity at least
![]() $1$
?
$1$
?
Notice that answering this question for hedgehogs of capacity exactly
![]() $1$
is sufficient, since the capacity satisfies
$1$
is sufficient, since the capacity satisfies
![]() $t(K_1)\le t(K_2)$
for any compact sets
$t(K_1)\le t(K_2)$
for any compact sets
![]() $K_1\subset K_2$
in
$K_1\subset K_2$
in
![]() $\mathbb C$
.
$\mathbb C$
.
In order to approach Question 1 we use a different construction of hedgehogs outlined in Eremenko’s post on the question in [Reference Lev5] with details set out in [Reference Schmidt6]. Any hedgehog
![]() $K=K(\beta _1,\dots ,\beta _n)$
of capacity precisely
$K=K(\beta _1,\dots ,\beta _n)$
of capacity precisely
![]() $1$
is in a bijective correspondence (up to rotation!) with the set of points
$1$
is in a bijective correspondence (up to rotation!) with the set of points
![]() $z_1,\dots ,z_n$
on the unit circle with prescribed positive real weights
$z_1,\dots ,z_n$
on the unit circle with prescribed positive real weights
![]() $r_1,\dots ,r_n$
satisfying
$r_1,\dots ,r_n$
satisfying
![]() $r_1+\dots +r_n=1$
. Namely, the mapping
$r_1+\dots +r_n=1$
. Namely, the mapping
 $$ \begin{align*}F(z)=\prod_{k=1}^n((z-z_k)(z^{-1}-\overline z_k))^{r_k} \end{align*} $$
$$ \begin{align*}F(z)=\prod_{k=1}^n((z-z_k)(z^{-1}-\overline z_k))^{r_k} \end{align*} $$
is a Riemann mapping of the complement of the closed unit disk to the complement
![]() $\hat {\mathbb C}\setminus K$
of hedgehog. It is not easy to write down the corresponding
$\hat {\mathbb C}\setminus K$
of hedgehog. It is not easy to write down the corresponding
![]() $\beta _j$
explicitly, but for their absolute values we get
$\beta _j$
explicitly, but for their absolute values we get
 $$ \begin{align*}|\beta_j|=\max_{z\in[z_{j-1},z_j]}|F(z)| =\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|^{2r_k} \quad\text{for}\; j=1,\dots,n, \end{align*} $$
$$ \begin{align*}|\beta_j|=\max_{z\in[z_{j-1},z_j]}|F(z)| =\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|^{2r_k} \quad\text{for}\; j=1,\dots,n, \end{align*} $$
where we conventionally take
![]() $z_0=z_n$
and understand
$z_0=z_n$
and understand
![]() $[z_{j-1},z_j]$
as arcs of the unit circle. This means that if
$[z_{j-1},z_j]$
as arcs of the unit circle. This means that if
![]() $C\ge 1$
is the minimum of
$C\ge 1$
is the minimum of
 $$ \begin{align*}\prod_{j=1}^n\max\bigg\{1,\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|^{r_k}\bigg\} \end{align*} $$
$$ \begin{align*}\prod_{j=1}^n\max\bigg\{1,\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|^{r_k}\bigg\} \end{align*} $$
taken over all n and all possible weighted configurations
![]() $z_1,\dots ,z_n$
, then
$z_1,\dots ,z_n$
, then
![]() $C^2$
is the minimum in Question 1.
$C^2$
is the minimum in Question 1.
Furthermore, in the spirit of [Reference Konyagin and Lev4] observe that from continuity considerations it suffices to compute the required minimum C for rational positive weights
![]() $r_1,\dots ,r_n$
. Assuming the latter and writing
$r_1,\dots ,r_n$
. Assuming the latter and writing
![]() $r_j=a_j/m$
for positive integers
$r_j=a_j/m$
for positive integers
![]() $a_1,\dots ,a_n$
and
$a_1,\dots ,a_n$
and
![]() $m=a_1+\dots +a_n$
, we look for the mth root of the minimum of
$m=a_1+\dots +a_n$
, we look for the mth root of the minimum of
 $$ \begin{align*}\prod_{j=1}^n\max\bigg\{1,\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|^{a_k}\bigg\} =\prod_{j=1}^m\max\bigg\{1,\max_{z\in[z_{j-1}',z_j']}\prod_{k=1}^m|z-z_k'|\bigg\}, \end{align*} $$
$$ \begin{align*}\prod_{j=1}^n\max\bigg\{1,\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|^{a_k}\bigg\} =\prod_{j=1}^m\max\bigg\{1,\max_{z\in[z_{j-1}',z_j']}\prod_{k=1}^m|z-z_k'|\bigg\}, \end{align*} $$
where
![]() $z_1',z_2',\dots ,z_m'$
is the multi-set
$z_1',z_2',\dots ,z_m'$
is the multi-set
 $$ \begin{align*}\underbrace{z_1,\dots,z_1}_{a_1 \;\text{times}}, \; \underbrace{z_2,\dots,z_2}_{a_2 \;\text{times}}, \; \dots, \; \underbrace{z_n,\dots,z_n}_{a_n \;\text{times}} \end{align*} $$
$$ \begin{align*}\underbrace{z_1,\dots,z_1}_{a_1 \;\text{times}}, \; \underbrace{z_2,\dots,z_2}_{a_2 \;\text{times}}, \; \dots, \; \underbrace{z_n,\dots,z_n}_{a_n \;\text{times}} \end{align*} $$
with prescribed weights all equal to 1. This means that it is enough to compute the minimum for the case of equal weights,
![]() $r_1=\dots =r_n=1/n$
, and we may give the following alternative formulation of Question 1.
$r_1=\dots =r_n=1/n$
, and we may give the following alternative formulation of Question 1.
Question 2. What is the minimum
![]() $C_n$
of
$C_n$
of
 $$ \begin{align*}\prod_{j=1}^n\max\bigg\{1,\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|\bigg\}^{1/n} \end{align*} $$
$$ \begin{align*}\prod_{j=1}^n\max\bigg\{1,\max_{z\in[z_{j-1},z_j]}\prod_{k=1}^n|z-z_k|\bigg\}^{1/n} \end{align*} $$
taken over all configurations of points
![]() $z_1,\dots ,z_n$
on the unit circle
$z_1,\dots ,z_n$
on the unit circle
![]() $|z|=1$
? The points are not required to be distinct and
$|z|=1$
? The points are not required to be distinct and
![]() $[z_{j-1},z_j]$
is understood as the corresponding arc of the circle,
$[z_{j-1},z_j]$
is understood as the corresponding arc of the circle,
![]() $z_0$
is identified with
$z_0$
is identified with
![]() $z_n$
.
$z_n$
.
Though there is no explicit requirement on the order of precedence, the minimum corresponds to the successive locations of
![]() $z_1,\dots ,z_n$
on the circle.
$z_1,\dots ,z_n$
on the circle.
A comparison with Dubinin’s result suggests that good candidates for the minima in Question 2 may originate from configurations in which all factors in the defining product but one are equal to
![]() $1$
. In our answer to the question we show that this is essentially the case by computing the related minima
$1$
. In our answer to the question we show that this is essentially the case by computing the related minima
![]() $C_n^*$
explicitly.
$C_n^*$
explicitly.
Theorem 3. For the quantity
![]() $C_n$
we have the inequality
$C_n$
we have the inequality
![]() $C_n\le C_n^*$
, where
$C_n\le C_n^*$
, where
![]() $C_n^*=(T_n(2^{1/n}))^{1/n}$
and
$C_n^*=(T_n(2^{1/n}))^{1/n}$
and
 $$ \begin{align*}T_n(x) =\sum_{k=0}^{\lfloor n/2\rfloor}\binom{n}{2k}(x^2-1)^kx^{n-2k} \end{align*} $$
$$ \begin{align*}T_n(x) =\sum_{k=0}^{\lfloor n/2\rfloor}\binom{n}{2k}(x^2-1)^kx^{n-2k} \end{align*} $$
denotes the nth Chebyshev polynomial of the first kind.
Theorem 4. For the quantity
![]() $C_n^*$
in Theorem 3 we have the asymptotic expansion
$C_n^*$
in Theorem 3 we have the asymptotic expansion
 $$ \begin{align*}C_n^*=1 + \nu - \frac14\nu^3 + \frac5{96}\nu^5 - \frac1{128}\nu^7 + O(\nu^9) \end{align*} $$
$$ \begin{align*}C_n^*=1 + \nu - \frac14\nu^3 + \frac5{96}\nu^5 - \frac1{128}\nu^7 + O(\nu^9) \end{align*} $$
in terms of
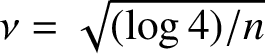 $\nu =\sqrt {(\log 4)/n}$
, as
$\nu =\sqrt {(\log 4)/n}$
, as
![]() $n\to \infty $
. In particular,
$n\to \infty $
. In particular,
 $(C_n^*)^{\sqrt n}\to e^{\sqrt {\log 4}}$
and
$(C_n^*)^{\sqrt n}\to e^{\sqrt {\log 4}}$
and
![]() $C_n^*\to 1$
as
$C_n^*\to 1$
as
![]() $n\to \infty $
.
$n\to \infty $
.
Thus, our results imply that the minimum in Question 1 is equal to
![]() $1$
, meaning that an analogue of Lehmer’s problem in an analytic setting is trivial. This has no consequences for Lehmer’s problem itself, as we are not aware of a recipe to cook up polynomials in
$1$
, meaning that an analogue of Lehmer’s problem in an analytic setting is trivial. This has no consequences for Lehmer’s problem itself, as we are not aware of a recipe to cook up polynomials in
![]() $\mathbb Z[x]$
from optimal (or near optimal) configurations of
$\mathbb Z[x]$
from optimal (or near optimal) configurations of
![]() $z_1,\dots ,z_n$
on the unit circle.
$z_1,\dots ,z_n$
on the unit circle.
3. Proofs
Proof of Theorem 3
We look for a configuration of the points
![]() $z_1,\dots ,z_n$
on the unit circle such that the maximum of
$z_1,\dots ,z_n$
on the unit circle such that the maximum of
![]() $|Q(z)|$
, where
$|Q(z)|$
, where
![]() $Q(z)=(z-z_1)\dotsb (z-z_n)$
, on all the arcs
$Q(z)=(z-z_1)\dotsb (z-z_n)$
, on all the arcs
![]() $[z_{j-1},z_j]$
but one is equal to
$[z_{j-1},z_j]$
but one is equal to
![]() $1$
:
$1$
:
 $$ \begin{align*}\max_{z\in[z_{j-1},z_j]}|Q(z)|=|Q(z_j^*)|=1 \quad\text{for}\; z_j^*\in(z_{j-1},z_j), \quad\text{where}\; j=2,\dots,n. \end{align*} $$
$$ \begin{align*}\max_{z\in[z_{j-1},z_j]}|Q(z)|=|Q(z_j^*)|=1 \quad\text{for}\; z_j^*\in(z_{j-1},z_j), \quad\text{where}\; j=2,\dots,n. \end{align*} $$
At the same time, the kth Chebyshev polynomial
![]() $T_k(x)=2^{k-1}x^k+\dotsb $
is known to satisfy
$T_k(x)=2^{k-1}x^k+\dotsb $
is known to satisfy
![]() $|T_k(x)|\le 1$
on the interval
$|T_k(x)|\le 1$
on the interval
![]() $-1\le x\le 1$
, with all the extrema on the interval being either
$-1\le x\le 1$
, with all the extrema on the interval being either
![]() $-1$
or
$-1$
or
![]() $1$
. Note that
$1$
. Note that
![]() $T_k(x)$
has k distinct real zeros on the open interval
$T_k(x)$
has k distinct real zeros on the open interval
![]() $-1<x<1$
and satisfies
$-1<x<1$
and satisfies
![]() $T_k(1)=(-1)^kT_k(-1)=1$
. Therefore, for
$T_k(1)=(-1)^kT_k(-1)=1$
. Therefore, for
![]() $n=2k$
even,
$n=2k$
even,
 $$ \begin{align*} Q(z)=z^k\,T_k\bigg(2^{1/k}\bigg(\frac{z+z^{-1}}2-1\bigg)+1\bigg), \end{align*} $$
$$ \begin{align*} Q(z)=z^k\,T_k\bigg(2^{1/k}\bigg(\frac{z+z^{-1}}2-1\bigg)+1\bigg), \end{align*} $$
we get a monic polynomial of degree n with the desired properties; its zeros
![]() $z_1,\dots ,z_n$
ordered in pairs, so that
$z_1,\dots ,z_n$
ordered in pairs, so that
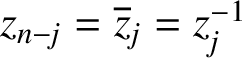 $z_{n-j}=\overline z_j=z_j^{-1}$
for
$z_{n-j}=\overline z_j=z_j^{-1}$
for
![]() $j=1,\dots ,k$
, correspond to the real zeros
$j=1,\dots ,k$
, correspond to the real zeros
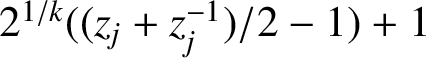 $2^{1/k}((z_j+z_j^{-1})/2-1)+1$
of the polynomial
$2^{1/k}((z_j+z_j^{-1})/2-1)+1$
of the polynomial
![]() $T_k(x)$
on the interval
$T_k(x)$
on the interval
![]() $-1<x<1$
. Then
$-1<x<1$
. Then
 $$ \begin{align*} \max_{z\in[z_n,z_1]}|Q(z)|=\max_{|z|=1}|Q(z)|=|Q(-1)| =|T_k(1-2^{1+1/k})|=T_k(2^{1+1/k}-1) =T_{2k}(2^{1/(2k)}), \end{align*} $$
$$ \begin{align*} \max_{z\in[z_n,z_1]}|Q(z)|=\max_{|z|=1}|Q(z)|=|Q(-1)| =|T_k(1-2^{1+1/k})|=T_k(2^{1+1/k}-1) =T_{2k}(2^{1/(2k)}), \end{align*} $$
where the duplication formula
![]() $T_k(2x^2-1)=T_{2k}(x)$
was applied.
$T_k(2x^2-1)=T_{2k}(x)$
was applied.
The duplication formula in fact allows one to write the very same polynomial
![]() $Q(z)$
in the form
$Q(z)$
in the form
 $$ \begin{align*}Q(z)=\pm (-z)^{n/2}\, T_n(2^{1/n - 1} {\textstyle\sqrt{2 - (z+z^{-1})}}\,), \end{align*} $$
$$ \begin{align*}Q(z)=\pm (-z)^{n/2}\, T_n(2^{1/n - 1} {\textstyle\sqrt{2 - (z+z^{-1})}}\,), \end{align*} $$
and this formula gives the desired polynomial, monic and of degree n, for n of any parity. If we set
![]() $k=\lfloor (n+1)/2\rfloor $
, the zeros
$k=\lfloor (n+1)/2\rfloor $
, the zeros
![]() $z_1,\dots ,z_n$
of
$z_1,\dots ,z_n$
of
![]() $Q(z)$
pair as before, that is,
$Q(z)$
pair as before, that is,
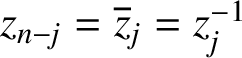 $z_{n-j}=\overline z_j=z_j^{-1}$
for
$z_{n-j}=\overline z_j=z_j^{-1}$
for
![]() $j=1,\dots ,k$
, with the two zeros merging into one,
$j=1,\dots ,k$
, with the two zeros merging into one,
![]() $z_{(n+1)/2}=1$
for
$z_{(n+1)/2}=1$
for
![]() $j=k$
when n is odd, so that
$j=k$
when n is odd, so that
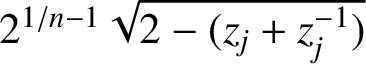 $2^{1/n - 1} \sqrt {2- \smash [b]{(z_j+z_j^{-1})}}$
for
$2^{1/n - 1} \sqrt {2- \smash [b]{(z_j+z_j^{-1})}}$
for
![]() $j=1,\dots ,k$
are precisely the k real zeros of the polynomial
$j=1,\dots ,k$
are precisely the k real zeros of the polynomial
![]() $T_n(x)$
on the interval
$T_n(x)$
on the interval
![]() $0\le x<1$
. This leads to the estimate
$0\le x<1$
. This leads to the estimate
 $$ \begin{align*}\max_{z\in[z_n,z_1]}|Q(z)|=\max_{|z|=1}|Q(z)|=|Q(-1)|=T_n(2^{1/n}) \end{align*} $$
$$ \begin{align*}\max_{z\in[z_n,z_1]}|Q(z)|=\max_{|z|=1}|Q(z)|=|Q(-1)|=T_n(2^{1/n}) \end{align*} $$
for both even and odd values of n.
Finally, we remark that the uniqueness of
![]() $Q(z)$
, up to rotation, follows from the extremal properties of the Chebyshev polynomials.
$Q(z)$
, up to rotation, follows from the extremal properties of the Chebyshev polynomials.
Proof of Theorem 4
For this part we cast the Chebyshev polynomial
![]() $T_n(x)$
in the form
$T_n(x)$
in the form
 $$ \begin{align*}T_n(x) =\frac{(x+\sqrt{x^2-1})^n+(x-\sqrt{x^2-1})^n}2 =\frac{x^n}2\cdot \textstyle((1+\sqrt{1-x^{-2}})^n+(1-\sqrt{1-x^{-2}})^n) \end{align*} $$
$$ \begin{align*}T_n(x) =\frac{(x+\sqrt{x^2-1})^n+(x-\sqrt{x^2-1})^n}2 =\frac{x^n}2\cdot \textstyle((1+\sqrt{1-x^{-2}})^n+(1-\sqrt{1-x^{-2}})^n) \end{align*} $$
leading to
 $$ \begin{align*}T_n(2^{1/n}) =\textstyle(1+\sqrt{1-e^{-\nu^2}})^n+(1-\sqrt{1-e^{-\nu^2}})^n \end{align*} $$
$$ \begin{align*}T_n(2^{1/n}) =\textstyle(1+\sqrt{1-e^{-\nu^2}})^n+(1-\sqrt{1-e^{-\nu^2}})^n \end{align*} $$
in the notation
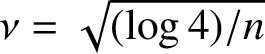 $\nu =\sqrt {(\log 4)/n}$
. Since
$\nu =\sqrt {(\log 4)/n}$
. Since
 $$ \begin{align*} {\textstyle\sqrt{1-e^{-\nu^2}}} &=\bigg(\sum_{k=1}^\infty\frac{(-1)^{k-1}\nu^{2k}}{k!}\bigg)^{\! 1/2} =\nu\bigg(1+\sum_{k=2}^\infty\frac{(-1)^{k-1}\nu^{2k-2}}{k!}\bigg)^{\! 1/2} \\ &=\nu\cdot\bigg(1 - \frac14\nu^2 + \frac5{96}\nu^4 - \frac1{128}\nu^6 + \frac{79}{92160}\nu^8 - \frac3{40960}\nu^{10}+O(\nu^{12})\bigg), \end{align*} $$
$$ \begin{align*} {\textstyle\sqrt{1-e^{-\nu^2}}} &=\bigg(\sum_{k=1}^\infty\frac{(-1)^{k-1}\nu^{2k}}{k!}\bigg)^{\! 1/2} =\nu\bigg(1+\sum_{k=2}^\infty\frac{(-1)^{k-1}\nu^{2k-2}}{k!}\bigg)^{\! 1/2} \\ &=\nu\cdot\bigg(1 - \frac14\nu^2 + \frac5{96}\nu^4 - \frac1{128}\nu^6 + \frac{79}{92160}\nu^8 - \frac3{40960}\nu^{10}+O(\nu^{12})\bigg), \end{align*} $$
we conclude that the term
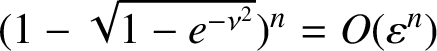 $(1-\sqrt {1-e^{-\nu ^2}})^n=O(\varepsilon ^n)$
for any choice of positive
$(1-\sqrt {1-e^{-\nu ^2}})^n=O(\varepsilon ^n)$
for any choice of positive
![]() $\varepsilon <1$
, hence
$\varepsilon <1$
, hence
 $$ \begin{align*} (T_n(2^{1/n}))^{1/n} =(1+\textstyle\sqrt{1-e^{-\nu^2}})\cdot(1+O(\varepsilon^n)), \end{align*} $$
$$ \begin{align*} (T_n(2^{1/n}))^{1/n} =(1+\textstyle\sqrt{1-e^{-\nu^2}})\cdot(1+O(\varepsilon^n)), \end{align*} $$
and the required asymptotics follows.
4. Speculations
Dimitrov’s estimate
![]() $t(K)\ge 1$
for the capacity of the hedgehog
$t(K)\ge 1$
for the capacity of the hedgehog
![]() $K=K(\beta _1,\dots ,\beta _n)$
assigned to a polynomial in
$K=K(\beta _1,\dots ,\beta _n)$
assigned to a polynomial in
![]() $\mathbb Z[x]$
is not necessarily sharp, and one would rather expect to have
$\mathbb Z[x]$
is not necessarily sharp, and one would rather expect to have
![]() $t(K)\ge t$
for some
$t(K)\ge t$
for some
![]() $t>1$
. By replacing the polynomial in the proof of Theorem 3 with
$t>1$
. By replacing the polynomial in the proof of Theorem 3 with
 $$ \begin{align*}Q(z)=\pm (-z)^{n/2}\, T_n(2^{1/n - 1}t {\textstyle\sqrt{2 - (z+z^{-1})}}\,) \end{align*} $$
$$ \begin{align*}Q(z)=\pm (-z)^{n/2}\, T_n(2^{1/n - 1}t {\textstyle\sqrt{2 - (z+z^{-1})}}\,) \end{align*} $$
and assuming (or, better, believing!) that the corresponding minimum in Question 2 is indeed attained in the case when all but one of the factors are equal to 1, we conclude that the minimum is equal to
![]() $(T_n(2^{1/n}t))^{\! 1/n}$
. The asymptotics of the Chebyshev polynomials then converts this result into the answer
$(T_n(2^{1/n}t))^{\! 1/n}$
. The asymptotics of the Chebyshev polynomials then converts this result into the answer
 $$ \begin{align*}\inf_{\substack{n=1,2,\dots\\ K = K(\beta_1, \dots, \beta_n)\\ t(K) \ge t}}\prod_{j=1}^n\max\{1,|\beta_j|\} \ge t+\textstyle\sqrt{t^2-1} \end{align*} $$
$$ \begin{align*}\inf_{\substack{n=1,2,\dots\\ K = K(\beta_1, \dots, \beta_n)\\ t(K) \ge t}}\prod_{j=1}^n\max\{1,|\beta_j|\} \ge t+\textstyle\sqrt{t^2-1} \end{align*} $$
to the related version of Question 1. This is slightly better, when
![]() $t>1$
, than the trivial estimate of the infimum by t from below.
$t>1$
, than the trivial estimate of the infimum by t from below.
In another direction, one may try to associate hedgehogs K to polynomials in a different (more involved!) way, to achieve some divisibility properties for the Hankel determinants
![]() $A_k$
that appear in the estimation
$A_k$
that appear in the estimation
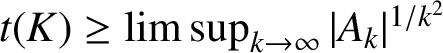 $t(K)\ge \limsup _{k\to \infty }|A_k|^{1/k^2}$
of the capacity on the basis of Pólya’s theorem. Such an approach has the potential to lead to some partial (‘Dobrowolski-type’) resolutions of Lehmer’s problem. Notice, however, that the bound for
$t(K)\ge \limsup _{k\to \infty }|A_k|^{1/k^2}$
of the capacity on the basis of Pólya’s theorem. Such an approach has the potential to lead to some partial (‘Dobrowolski-type’) resolutions of Lehmer’s problem. Notice, however, that the bound for
![]() $t(K)$
in Pólya’s theorem is not sharp: numerically, the Hankel determinants
$t(K)$
in Pólya’s theorem is not sharp: numerically, the Hankel determinants
![]() $A_k=\det _{0\le i,j<k}(a_{i+j})$
constructed on (Dimitrov’s) irrational series
$A_k=\det _{0\le i,j<k}(a_{i+j})$
constructed on (Dimitrov’s) irrational series

for Smyth’s polynomial
![]() $x^3-x-1=(x-\alpha _1)(x-\alpha _2)(x-\alpha _3)$
satisfy
$x^3-x-1=(x-\alpha _1)(x-\alpha _2)(x-\alpha _3)$
satisfy
![]() $|A_k|\le C^k$
for some
$|A_k|\le C^k$
for some
![]() $C<2.5$
and all
$C<2.5$
and all
![]() $k\le 150$
, so that it is likely that
$k\le 150$
, so that it is likely that
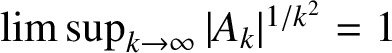 $\limsup _{k\to \infty }|A_k|^{1/k^2}=1$
in this case.
$\limsup _{k\to \infty }|A_k|^{1/k^2}=1$
in this case.
Acknowledgement
The third author thanks Yuri Bilu and Laurent Habsieger for inspirational conversations on the Lehmer and Schinzel–Zassenhaus problems.



