Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T04:12:55.452Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorffness in varieties of topological groups

Published online by Cambridge University Press:  17 April 2009

Carolyn E. McPhail
Carolyn E. McPhail
Affiliation:
Department of MathematicsUniversity of WollongongWollongong NSW 2522Australia e-mail: caz_mcphail@uow. edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A variety of topological groups 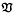is a class of (not necessarily Hausdorff) topological groups closed under the operations of forming subgroups, quotient groups and arbitrary products. It is well known that the class of groups underlying the topological groups contained in any variety of topological groups is a variety of groups. Much work on topological groups is restricted to Hausdorff topological groups and so it is relevant to know if the class of groups underlying Hausdorff topological groups in 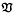is a variety of groups. It is shown that this is not always the case. Indeed it is proved that this is not the case for an important proper class of varieties of topological groups.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 57 , Issue 1 , February 1998 , pp. 147 - 151
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Hewitt, E. and Ross, K.A., Abstract harmonic analysis I (Springer-Verlag, Berlin, Heidelberg, New York, 1963).Google Scholar
[2]Higman, G., ‘On finite simple permutation groups’, Publ. Math. Debrecen 3 (1954), 221–226.CrossRefGoogle Scholar
[3]Kopperman, R.D., Mislove, M.W., Morris, S.A., Nickolas, P., Pestov, V. and Svetlichny, S., ‘Limit laws for wide varieties of topological groups’, Houston J. Math 2 (1996), 307–328.Google Scholar
[4]Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory: Presentations of groups in terms of generators and relations (Dover Publications Inc., New York, 1976).Google Scholar
[5]Morris, S.A., ‘Varieties of topological groups’, Bull. Austral. Math. Soc. 1 (1969), 145–160.CrossRefGoogle Scholar
[6]Morris, S.A., ‘Varieties of topological groups III’, Bull. Austral. Math. Soc. 2 (1970), 165–178.CrossRefGoogle Scholar
[7]Morris, S.A., Pontryagin duality and the structure of locally compact Abelian groups (Cambridge University Press, Cambridge, 1977).CrossRefGoogle Scholar
[8]Morris, S.A., ‘Varieties of topological groups – A survey’, Colloq. Math. 46 (1982), 147–165.CrossRefGoogle Scholar
[9]Neumann, H., Varieties of groups (Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar