Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T21:57:39.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic sets and the harmonic prime number theorem

Published online by Cambridge University Press:  17 April 2009

Kevin A. Broughan  and
Rory J. Casey
Kevin A. Broughan
Affiliation:
Department of Mathematics, University of Waikato, Hamilton, New Zealand, e-mail: [email protected]
Rory J. Casey
Affiliation:
Department of Mathematics, University of Waikato, Hamilton, New Zealand, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We restrict primes and prime powers to sets 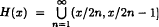. Let 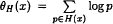. Then the error in θH(x) has, unconditionally, the expected order of magnitude 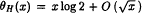. However, if 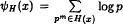then ψH (x) = x log 2 + O (log x). Some reasons for and consequences of these sharp results are explored. A proof is given of the “harmonic prime number theorem”, πH (x)/π (x) → log 2.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 71 , Issue 1 , February 2005 , pp. 127 - 137
Copyright
Copyright © Australian Mathematical Society 2005

References

[1]Broughan, K.A., ‘Asymptotic order of the squarefree part of n!’, Integers (electronic) 2 (2002), 1–6.Google Scholar
[2]Edwards, T.M., Riemann's zeta function (Dover, New York, 1974).Google Scholar
[3]Heath-Brown, D.R., ‘Sieve identities and gaps between primes’, J. Arithmètiques (1981), 61–65.Google Scholar
[4]Sárközy, A., ‘On divisors of binomial coefficients I’, J. Number Theory 20 (1985), 70–80.CrossRefGoogle Scholar