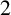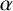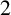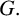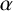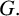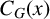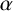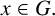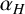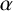1 Introduction
Throughout this paper, G will denote a finite group.
Definition 1.1. A
![]() $2$
-cocycle of G over
$2$
-cocycle of G over
![]() $\mathbb {C}$
is a function
$\mathbb {C}$
is a function
![]() $\alpha : G\times G\rightarrow \mathbb {C}^*$
such that
$\alpha : G\times G\rightarrow \mathbb {C}^*$
such that
![]() $\alpha (x, 1) = 1$
and
$\alpha (x, 1) = 1$
and
![]() $\alpha (x, y)\alpha (xy, z) = \alpha (x, yz)\alpha (y, z)$
for all x, y,
$\alpha (x, y)\alpha (xy, z) = \alpha (x, yz)\alpha (y, z)$
for all x, y,
![]() $z\in G.$
$z\in G.$
The set of all such
![]() $2$
-cocycles of G forms a group
$2$
-cocycles of G forms a group
![]() $Z^2(G, \mathbb {C}^*)$
under multiplication. Let
$Z^2(G, \mathbb {C}^*)$
under multiplication. Let
![]() $\delta : G\rightarrow \mathbb {C}^*$
be any function with
$\delta : G\rightarrow \mathbb {C}^*$
be any function with
![]() $\delta (1) = 1.$
Then
$\delta (1) = 1.$
Then
![]() $t(\delta )(x, y) = \delta (x)\delta (y)/\delta (xy)$
for all
$t(\delta )(x, y) = \delta (x)\delta (y)/\delta (xy)$
for all
![]() $x, y\in G$
is a
$x, y\in G$
is a
![]() $2$
-cocycle of G, which is called a coboundary. Two
$2$
-cocycle of G, which is called a coboundary. Two
![]() $2$
-cocycles
$2$
-cocycles
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are cohomologous if there exists a coboundary
$\beta $
are cohomologous if there exists a coboundary
![]() $t(\delta )$
such that
$t(\delta )$
such that
![]() $\beta = t(\delta )\alpha .$
This defines an equivalence relation on
$\beta = t(\delta )\alpha .$
This defines an equivalence relation on
![]() $Z^2(G, \mathbb {C}^*)$
and the cohomology classes
$Z^2(G, \mathbb {C}^*)$
and the cohomology classes
![]() $[\alpha ]$
form a finite abelian group, called the Schur multiplier
$[\alpha ]$
form a finite abelian group, called the Schur multiplier
![]() $M(G).$
$M(G).$
Definition 1.2. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $G.$
Then
$G.$
Then
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if
$\alpha $
-regular if
![]() $\alpha (x, g) = \alpha (g, x)$
for all
$\alpha (x, g) = \alpha (g, x)$
for all
![]() $g\in C_G(x).$
$g\in C_G(x).$
Obviously, if
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular, then it is
$\alpha $
-regular, then it is
![]() $\alpha ^k$
-regular for any integer
$\alpha ^k$
-regular for any integer
![]() $k;$
also setting
$k;$
also setting
![]() $y = 1$
and
$y = 1$
and
![]() $z = x$
in Definition 1.1 yields
$z = x$
in Definition 1.1 yields
![]() $\alpha (1, x) = 1$
for all
$\alpha (1, x) = 1$
for all
![]() $x\in G$
and hence
$x\in G$
and hence
![]() $1$
is
$1$
is
![]() $\alpha $
-regular. Let
$\alpha $
-regular. Let
![]() $\beta \in [\alpha ]$
. Then x is
$\beta \in [\alpha ]$
. Then x is
![]() $\alpha $
-regular if and only if it is
$\alpha $
-regular if and only if it is
![]() $\beta $
-regular and any conjugate of x is also
$\beta $
-regular and any conjugate of x is also
![]() $\alpha $
-regular (see [Reference Karpilovsky5, Lemma 2.6.1]), so that one may refer to the
$\alpha $
-regular (see [Reference Karpilovsky5, Lemma 2.6.1]), so that one may refer to the
![]() $\alpha $
-regular conjugacy classes of
$\alpha $
-regular conjugacy classes of
![]() $G.$
Using this notation and
$G.$
Using this notation and
![]() $o(\phantom {.})$
for the order of a group element, we quote [Reference Higgs3, Lemma 1.2(b)] for future reference.
$o(\phantom {.})$
for the order of a group element, we quote [Reference Higgs3, Lemma 1.2(b)] for future reference.
Lemma 1.3. Suppose
![]() $o(x)$
and
$o(x)$
and
![]() $o([\alpha ])$
are relatively prime. Then x is
$o([\alpha ])$
are relatively prime. Then x is
![]() $\alpha $
-regular.
$\alpha $
-regular.
Let H be a subgroup of
![]() $G.$
Given a
$G.$
Given a
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
of G, one can define the
$\alpha $
of G, one can define the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha _H$
of H by
$\alpha _H$
of H by
![]() $\alpha _H(x, y) = \alpha (x, y)$
for all
$\alpha _H(x, y) = \alpha (x, y)$
for all
![]() $x, y\in H.$
The mapping from
$x, y\in H.$
The mapping from
![]() $Z^2(G, \mathbb {C}^*)\rightarrow Z^2(H, \mathbb {C}^*)$
defined by
$Z^2(G, \mathbb {C}^*)\rightarrow Z^2(H, \mathbb {C}^*)$
defined by
![]() $\alpha \mapsto \alpha _H$
maps coboundaries of G to those of H and consequently induces the restriction homomorphism
$\alpha \mapsto \alpha _H$
maps coboundaries of G to those of H and consequently induces the restriction homomorphism
![]() $\operatorname {\mathrm {Res}}_{G, H}: M(G)\rightarrow M(H)$
defined by
$\operatorname {\mathrm {Res}}_{G, H}: M(G)\rightarrow M(H)$
defined by
![]() $[\alpha ]\mapsto [\alpha _H].$
Clearly, an element
$[\alpha ]\mapsto [\alpha _H].$
Clearly, an element
![]() $h\in H$
that is
$h\in H$
that is
![]() $\alpha $
-regular in G is
$\alpha $
-regular in G is
![]() $\alpha _H$
-regular, but the converse is in general false. The twin aims of this paper are to find conditions under which first there exists a nontrivial element of H that is
$\alpha _H$
-regular, but the converse is in general false. The twin aims of this paper are to find conditions under which first there exists a nontrivial element of H that is
![]() $\alpha $
-regular in G and second that every
$\alpha $
-regular in G and second that every
![]() $\alpha _H$
-regular element of H is
$\alpha _H$
-regular element of H is
![]() $\alpha $
-regular in
$\alpha $
-regular in
![]() $G.$
$G.$
There are some circumstances in which it is possible to produce a nontrivial element
![]() $x\in G$
that is
$x\in G$
that is
![]() $\alpha $
-regular for all
$\alpha $
-regular for all
![]() $[\alpha ]\in M(G).$
For example, this is true if
$[\alpha ]\in M(G).$
For example, this is true if
![]() $C_G(x) = \langle x\rangle ,$
since the Schur multiplier of a cyclic group is trivial (see [Reference Karpilovsky4, Proposition 2.1.1]). However, in general,
$C_G(x) = \langle x\rangle ,$
since the Schur multiplier of a cyclic group is trivial (see [Reference Karpilovsky4, Proposition 2.1.1]). However, in general,
![]() $\alpha $
-regularity very much depends upon the choice of
$\alpha $
-regularity very much depends upon the choice of
![]() $[\alpha ]$
as the next example demonstrates, using the inflation homomorphism. Let N be a normal subgroup of G. Then the mapping from
$[\alpha ]$
as the next example demonstrates, using the inflation homomorphism. Let N be a normal subgroup of G. Then the mapping from
![]() $Z^2(G/N, \mathbb {C}^*)\rightarrow Z^2(G, \mathbb {C}^*),\, \beta \mapsto \alpha ,$
where
$Z^2(G/N, \mathbb {C}^*)\rightarrow Z^2(G, \mathbb {C}^*),\, \beta \mapsto \alpha ,$
where
![]() $\alpha (x, y) = \beta (xN, yN)$
for all
$\alpha (x, y) = \beta (xN, yN)$
for all
![]() $x, y\in G$
maps coboundaries of
$x, y\in G$
maps coboundaries of
![]() $G/N$
to those of G and hence induces
$G/N$
to those of G and hence induces
![]() $\operatorname {\mathrm {Inf}}: M(G/N)\rightarrow M(G), [\beta ]\mapsto [\alpha ].$
Using this notation, it is clear that every element of N is
$\operatorname {\mathrm {Inf}}: M(G/N)\rightarrow M(G), [\beta ]\mapsto [\alpha ].$
Using this notation, it is clear that every element of N is
![]() $\alpha $
-regular.
$\alpha $
-regular.
Example 1.4. Let
![]() $C_n^{(m)}$
denote the direct product of m copies of the cyclic group of order
$C_n^{(m)}$
denote the direct product of m copies of the cyclic group of order
![]() $n.$
Let
$n.$
Let
![]() $G\cong C_{n_1}\times \cdots \times C_{n_k},$
where
$G\cong C_{n_1}\times \cdots \times C_{n_k},$
where
![]() $n_{i+1}\mid n_i$
for
$n_{i+1}\mid n_i$
for
![]() $i = 1,\ldots , k-1$
and
$i = 1,\ldots , k-1$
and
![]() $k\geq 2.$
Then
$k\geq 2.$
Then
![]() $M(G) \cong C_{n_2}\times C_{n_3}^{(2)}\times \cdots \times C_{n_k}^{(k-1)}$
(see [Reference Karpilovsky4, Corollary 2.2.12]). Also, the group of elements that are
$M(G) \cong C_{n_2}\times C_{n_3}^{(2)}\times \cdots \times C_{n_k}^{(k-1)}$
(see [Reference Karpilovsky4, Corollary 2.2.12]). Also, the group of elements that are
![]() $\alpha $
-regular for all
$\alpha $
-regular for all
![]() $[\alpha ]\in M(G)$
is isomorphic to
$[\alpha ]\in M(G)$
is isomorphic to
![]() $C_{n_1/n_2}$
(see [Reference Karpilovsky5, Theorem 11.8.19]). Let
$C_{n_1/n_2}$
(see [Reference Karpilovsky5, Theorem 11.8.19]). Let
![]() $R\cong C_2^{(2)},$
then
$R\cong C_2^{(2)},$
then
![]() $M(R)\cong C_2$
and so only the trivial element of
$M(R)\cong C_2$
and so only the trivial element of
![]() $C_2^{(2)}$
is
$C_2^{(2)}$
is
![]() $\alpha $
-regular for
$\alpha $
-regular for
![]() $[\alpha ]$
nontrivial. However, if
$[\alpha ]$
nontrivial. However, if
![]() $H \neq R$
is a subgroup of R, then every element of H is
$H \neq R$
is a subgroup of R, then every element of H is
![]() $\alpha _H$
-regular. Now let
$\alpha _H$
-regular. Now let
![]() $S \cong C_2^{(3)},$
so that
$S \cong C_2^{(3)},$
so that
![]() $M(S)\cong C_2^{(3)}.$
Let x be a nontrivial element of
$M(S)\cong C_2^{(3)}.$
Let x be a nontrivial element of
![]() $S.$
Then
$S.$
Then
![]() $\operatorname {\mathrm {Inf}}: M(S/\langle x\rangle )\rightarrow M(S)$
is an injective map (see [Reference Karpilovsky4, Theorem 2.3.10]) that produces a subgroup
$\operatorname {\mathrm {Inf}}: M(S/\langle x\rangle )\rightarrow M(S)$
is an injective map (see [Reference Karpilovsky4, Theorem 2.3.10]) that produces a subgroup
![]() $\langle [\alpha ]\rangle $
of order
$\langle [\alpha ]\rangle $
of order
![]() $2$
of
$2$
of
![]() $M(S)$
in which
$M(S)$
in which
![]() $1$
and x are the only
$1$
and x are the only
![]() $\alpha $
-regular elements. Thus, for any two different nontrivial elements
$\alpha $
-regular elements. Thus, for any two different nontrivial elements
![]() $[\alpha ], [\beta ]\in M(S)$
, the intersection of the set of
$[\alpha ], [\beta ]\in M(S)$
, the intersection of the set of
![]() $\alpha $
-regular elements and
$\alpha $
-regular elements and
![]() $\beta $
-regular elements of S contains only the identity element.
$\beta $
-regular elements of S contains only the identity element.
2 Subgroups and regularity
Definition 2.1. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $G.$
Then an
$G.$
Then an
![]() $\alpha $
-representation of G of dimension n is a function
$\alpha $
-representation of G of dimension n is a function
![]() $P:G\rightarrow GL(n, \mathbb {C})$
such that
$P:G\rightarrow GL(n, \mathbb {C})$
such that
![]() $P(x)P(y) = \alpha (x, y)P(xy)$
for all x,
$P(x)P(y) = \alpha (x, y)P(xy)$
for all x,
![]() $y\in G.$
$y\in G.$
An
![]() $\alpha $
-representation P is also called a projective representation of G with
$\alpha $
-representation P is also called a projective representation of G with
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha ,$
its trace function
$\alpha ,$
its trace function
![]() $\xi $
is its
$\xi $
is its
![]() $\alpha $
-character and
$\alpha $
-character and
![]() $\xi (1),$
which is the dimension of
$\xi (1),$
which is the dimension of
![]() $P,$
is called the degree of
$P,$
is called the degree of
![]() $\xi .$
$\xi .$
To avoid repetition, all
![]() $\alpha $
-representations of G in this section are defined over
$\alpha $
-representations of G in this section are defined over
![]() $\mathbb {C}.$
Let
$\mathbb {C}.$
Let
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
denote the set of all irreducible
$\operatorname {\mathrm {Proj}}(G, \alpha )$
denote the set of all irreducible
![]() $\alpha $
-characters of
$\alpha $
-characters of
![]() $G,$
the relationship between
$G,$
the relationship between
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
and
$\operatorname {\mathrm {Proj}}(G, \alpha )$
and
![]() $\alpha $
-representations is much the same as that between
$\alpha $
-representations is much the same as that between
![]() $\operatorname {\mathrm {Irr}}(G)$
and (ordinary) representations of G (see [Reference Karpilovsky5, page 184] for details) so, for example,
$\operatorname {\mathrm {Irr}}(G)$
and (ordinary) representations of G (see [Reference Karpilovsky5, page 184] for details) so, for example,
![]() $\sum _{\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )}\xi (1)^2 = \vert G\vert $
(see [Reference Karpilovsky6, Lemma 1.4.4]). Next,
$\sum _{\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )}\xi (1)^2 = \vert G\vert $
(see [Reference Karpilovsky6, Lemma 1.4.4]). Next,
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if and only if
$\alpha $
-regular if and only if
![]() $\xi (x)\not = 0$
for some
$\xi (x)\not = 0$
for some
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
(see [Reference Karpilovsky6, Proposition 1.6.3]) and
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
(see [Reference Karpilovsky6, Proposition 1.6.3]) and
![]() $\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert $
is the number of
$\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert $
is the number of
![]() $\alpha $
-regular conjugacy classes of G (see [Reference Karpilovsky6, Theorem 1.3.6]).
$\alpha $
-regular conjugacy classes of G (see [Reference Karpilovsky6, Theorem 1.3.6]).
For
![]() $[\beta ]{\kern-1pt}\in{\kern-1pt} M(G)$
, there exists
$[\beta ]{\kern-1pt}\in{\kern-1pt} M(G)$
, there exists
![]() $\alpha {\kern-1pt}\in{\kern-1pt} [\beta ]$
such that
$\alpha {\kern-1pt}\in{\kern-1pt} [\beta ]$
such that
![]() $o(\alpha ) {\kern-1pt}={\kern-1pt} o([\beta ])$
and
$o(\alpha ) {\kern-1pt}={\kern-1pt} o([\beta ])$
and
![]() $\alpha $
is class-preserving, that is, the elements of
$\alpha $
is class-preserving, that is, the elements of
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
are class functions (see [Reference Karpilovsky6, Corollary 4.1.6]). Henceforward, it will be assumed, without loss of generality, that the initial choice of
$\operatorname {\mathrm {Proj}}(G, \alpha )$
are class functions (see [Reference Karpilovsky6, Corollary 4.1.6]). Henceforward, it will be assumed, without loss of generality, that the initial choice of
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
has these two properties. Under these assumptions, the ‘standard’ inner product
$\alpha $
has these two properties. Under these assumptions, the ‘standard’ inner product
![]() $\langle \phantom {\xi }, \phantom {.}\rangle $
may be defined on
$\langle \phantom {\xi }, \phantom {.}\rangle $
may be defined on
![]() $\alpha _H$
-characters of subgroups H of G and the ‘normal’ orthogonality relations hold (see [Reference Karpilovsky6, Section 1.11.D]).
$\alpha _H$
-characters of subgroups H of G and the ‘normal’ orthogonality relations hold (see [Reference Karpilovsky6, Section 1.11.D]).
The main result in this section is the following simple observation.
Lemma 2.2. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G and let H be a subgroup of
$2$
-cocycle of G and let H be a subgroup of
![]() $G.$
Let
$G.$
Let
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
![]() $\gamma \in \operatorname {\mathrm {Proj}}(H, \alpha _H).$
Suppose that either
$\gamma \in \operatorname {\mathrm {Proj}}(H, \alpha _H).$
Suppose that either
![]() $\langle \xi _H, \gamma \rangle = 0$
or
$\langle \xi _H, \gamma \rangle = 0$
or
![]() $\vert H\vert \nmid \xi (1)\gamma (1).$
Then there exists a nontrivial
$\vert H\vert \nmid \xi (1)\gamma (1).$
Then there exists a nontrivial
![]() $h\in H$
such that
$h\in H$
such that
![]() $\xi (h)\overline {\gamma (h)}\not = 0$
and, in particular, all such elements are
$\xi (h)\overline {\gamma (h)}\not = 0$
and, in particular, all such elements are
![]() $\alpha $
-regular in
$\alpha $
-regular in
![]() $G.$
$G.$
Proof. The inner product of
![]() $\xi _H$
and
$\xi _H$
and
![]() $\gamma ,$
which is a nonnegative integer, is defined by
$\gamma ,$
which is a nonnegative integer, is defined by
 $$ \begin{align*}\langle \xi_H, \gamma \rangle = \frac{1}{\vert H\vert}\bigg(\xi(1)\gamma(1) + \sum_{h\in H -\{1\}}\xi(h)\overline{\gamma(h)}\bigg).\end{align*} $$
$$ \begin{align*}\langle \xi_H, \gamma \rangle = \frac{1}{\vert H\vert}\bigg(\xi(1)\gamma(1) + \sum_{h\in H -\{1\}}\xi(h)\overline{\gamma(h)}\bigg).\end{align*} $$
Thus, under the two specified conditions, the summation on the right-hand side must be nonzero.
Using Frobenius reciprocity, similar results can be obtained to those in Lemma 2.2 using induction instead of restriction and replacing
![]() $\vert H\vert $
by
$\vert H\vert $
by
![]() $\vert G\vert .$
$\vert G\vert .$
Corollary 2.3. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G and let P be a Sylow p-subgroup of
$2$
-cocycle of G and let P be a Sylow p-subgroup of
![]() $G.$
$G.$
-
(a) Suppose that G contains a nontrivial
 $\alpha $
-regular element. Then G contains a nontrivial
$\alpha $
-regular element. Then G contains a nontrivial
 $\alpha $
-regular element of prime power order.
$\alpha $
-regular element of prime power order. -
(b) Suppose that P contains a nontrivial
 $\alpha _P$
-regular element. Then P contains a nontrivial
$\alpha _P$
-regular element. Then P contains a nontrivial
 $\alpha $
-regular element of
$\alpha $
-regular element of
 $G.$
$G.$
Proof. Let
![]() $c_{\alpha }(G)$
denote the greatest common divisor of the degrees of the elements of
$c_{\alpha }(G)$
denote the greatest common divisor of the degrees of the elements of
![]() $\operatorname {\mathrm {Proj}}(G, \alpha ).$
Then
$\operatorname {\mathrm {Proj}}(G, \alpha ).$
Then
![]() $(c_{\alpha }(G))_p = \min \{\gamma (1): \gamma \in \operatorname {\mathrm {Proj}}(P, \alpha _P)\}$
(see [Reference Karpilovsky6, Lemma 1.4.11]), where
$(c_{\alpha }(G))_p = \min \{\gamma (1): \gamma \in \operatorname {\mathrm {Proj}}(P, \alpha _P)\}$
(see [Reference Karpilovsky6, Lemma 1.4.11]), where
![]() $n_p$
denotes the pth part of
$n_p$
denotes the pth part of
![]() $n.$
$n.$
For item (a),
![]() $\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert> 1$
and so there exists a prime number q such that
$\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert> 1$
and so there exists a prime number q such that
![]() $(c_{\alpha }(G))_q^2 < \vert Q\vert ,$
where Q is a Sylow q-subgroup of
$(c_{\alpha }(G))_q^2 < \vert Q\vert ,$
where Q is a Sylow q-subgroup of
![]() $G.$
Let
$G.$
Let
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and let
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and let
![]() $\gamma \in \operatorname {\mathrm {Proj}}(Q, \alpha _Q)$
with
$\gamma \in \operatorname {\mathrm {Proj}}(Q, \alpha _Q)$
with
![]() $(\xi (1))_q = \gamma (1) = (c_{\alpha }(G))_q.$
Then Q contains a nontrivial
$(\xi (1))_q = \gamma (1) = (c_{\alpha }(G))_q.$
Then Q contains a nontrivial
![]() $\alpha $
-regular element of G from Lemma 2.2.
$\alpha $
-regular element of G from Lemma 2.2.
For item (b),
![]() $\vert \!\operatorname {\mathrm {Proj}}(P, \alpha _P)\vert> 1$
and the proof is the same as for item (a).
$\vert \!\operatorname {\mathrm {Proj}}(P, \alpha _P)\vert> 1$
and the proof is the same as for item (a).
These results give little control over the nontrivial
![]() $\alpha $
-regular element of G produced, so in the next section, we will seek conditions under which a given element of G is
$\alpha $
-regular element of G produced, so in the next section, we will seek conditions under which a given element of G is
![]() $\alpha $
-regular.
$\alpha $
-regular.
3 Hall subgroups and regularity
Let H be a subgroup of G and let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $H.$
Then for
$H.$
Then for
![]() $g\in G$
, one can define the
$g\in G$
, one can define the
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha ^g$
of
$\alpha ^g$
of
![]() $Z^2(gHg^{-1}, \mathbb {C}^*)$
by
$Z^2(gHg^{-1}, \mathbb {C}^*)$
by
![]() $\alpha ^g(x, y)= \alpha (g^{-1}xg, g^{-1}yg)$
for all
$\alpha ^g(x, y)= \alpha (g^{-1}xg, g^{-1}yg)$
for all
![]() $x, y\in gHg^{-1}.$
The mapping from
$x, y\in gHg^{-1}.$
The mapping from
![]() $Z^2(H, \mathbb {C}^*)\rightarrow Z^2(gHg^{-1}, \mathbb {C}^*)$
defined by
$Z^2(H, \mathbb {C}^*)\rightarrow Z^2(gHg^{-1}, \mathbb {C}^*)$
defined by
![]() $\alpha \mapsto \alpha ^g$
maps coboundaries of H to those of
$\alpha \mapsto \alpha ^g$
maps coboundaries of H to those of
![]() $gHg^{-1}$
and therefore induces a homomorphism called conjugation by
$gHg^{-1}$
and therefore induces a homomorphism called conjugation by
![]() $g, \operatorname {\mathrm {Con}}_H^g: M(H)\rightarrow M(gHg^{-1})$
defined by
$g, \operatorname {\mathrm {Con}}_H^g: M(H)\rightarrow M(gHg^{-1})$
defined by
![]() $[\alpha ]\mapsto [\alpha ^g].$
So, in particular,
$[\alpha ]\mapsto [\alpha ^g].$
So, in particular,
![]() $h\in H$
is
$h\in H$
is
![]() $\alpha $
-regular if and only if
$\alpha $
-regular if and only if
![]() $ghg^{-1}$
is
$ghg^{-1}$
is
![]() $\alpha ^g$
-regular in
$\alpha ^g$
-regular in
![]() $gHg^{-1}.$
Next,
$gHg^{-1}.$
Next,
![]() $[\alpha ]$
is G-stable if for all
$[\alpha ]$
is G-stable if for all
![]() $g\in G,$
$g\in G,$
where
![]() $H(g) = H\cap gHg^{-1}.$
The G-stable elements of
$H(g) = H\cap gHg^{-1}.$
The G-stable elements of
![]() $M(H)$
form a subgroup
$M(H)$
form a subgroup
![]() $M(H)^G$
of
$M(H)^G$
of
![]() $M(H).$
In the next result, another homomorphism is mentioned, this is corestriction from
$M(H).$
In the next result, another homomorphism is mentioned, this is corestriction from
![]() $M(H)$
into
$M(H)$
into
![]() $M(G),$
but as it will not subsequently be used, the reader is referred to [Reference Karpilovsky4, page 10] for details.
$M(G),$
but as it will not subsequently be used, the reader is referred to [Reference Karpilovsky4, page 10] for details.
Next, some notation and definitions. Let
![]() $\pi $
denote a set of prime numbers and let n be a positive integer. Then
$\pi $
denote a set of prime numbers and let n be a positive integer. Then
![]() $n_{\pi}$
denotes the
$n_{\pi}$
denotes the
![]() $\pi $
th part of n and n is a
$\pi $
th part of n and n is a
![]() $\pi $
-number if
$\pi $
-number if
![]() $n_{\pi } = n.$
An element
$n_{\pi } = n.$
An element
![]() $x\in G$
and a (sub)group H of G are a
$x\in G$
and a (sub)group H of G are a
![]() $\pi $
-element and
$\pi $
-element and
![]() $\pi $
-(sub)group if
$\pi $
-(sub)group if
![]() $o(x)$
and
$o(x)$
and
![]() $\vert H\vert $
are respectively
$\vert H\vert $
are respectively
![]() $\pi $
-numbers. Also let
$\pi $
-numbers. Also let
![]() $x_{\pi }$
and
$x_{\pi }$
and
![]() $x_{\pi '}$
be the unique elements in
$x_{\pi '}$
be the unique elements in
![]() $\langle x\rangle $
such that
$\langle x\rangle $
such that
![]() $x = x_{\pi }x_{\pi '}$
with
$x = x_{\pi }x_{\pi '}$
with
![]() $o(x_{\pi })$
a
$o(x_{\pi })$
a
![]() $\pi $
-number and
$\pi $
-number and
![]() $o(x_{\pi '})$
a
$o(x_{\pi '})$
a
![]() $\pi '$
-number, where
$\pi '$
-number, where
![]() $\pi '$
is the complement to
$\pi '$
is the complement to
![]() $\pi $
in the set of all prime numbers. A Sylow
$\pi $
in the set of all prime numbers. A Sylow
![]() $\pi $
-subgroup S of G is a maximal
$\pi $
-subgroup S of G is a maximal
![]() $\pi $
-subgroup of
$\pi $
-subgroup of
![]() $G; S$
is a Hall
$G; S$
is a Hall
![]() $\pi $
-subgroup of G if, in addition,
$\pi $
-subgroup of G if, in addition,
![]() $\vert G : S\vert $
is relatively prime to
$\vert G : S\vert $
is relatively prime to
![]() $\vert S\vert .$
The first result generalises to Hall subgroups a theorem on the connection between the Schur multiplier of G and those of its Sylow subgroups (see [Reference Karpilovsky4, Theorem 2.1.2]).
$\vert S\vert .$
The first result generalises to Hall subgroups a theorem on the connection between the Schur multiplier of G and those of its Sylow subgroups (see [Reference Karpilovsky4, Theorem 2.1.2]).
Proposition 3.1. Suppose H is a Hall
![]() $\pi $
-subgroup of
$\pi $
-subgroup of
![]() $G.$
Then:
$G.$
Then:
-
(a) corestriction from
 $M(H)$
into
$M(H)$
into
 $M(G)$
maps
$M(G)$
maps
 $M(H)^G$
isomorphically onto the Hall
$M(H)^G$
isomorphically onto the Hall
 $\pi $
-subgroup of
$\pi $
-subgroup of
 $M(G)$
;
$M(G)$
; -
(b) restriction from
 $M(G)$
into
$M(G)$
into
 $M(H)$
induces an injective homomorphism,
$M(H)$
induces an injective homomorphism,
 $\operatorname {\mathrm {res}}$
, from the Hall
$\operatorname {\mathrm {res}}$
, from the Hall
 $\pi $
-subgroup of
$\pi $
-subgroup of
 $M(G)$
into
$M(G)$
into
 $M(H)$
;
$M(H)$
; -
(c)
 $M(H)^G$
is a direct factor of
$M(H)^G$
is a direct factor of
 $M(H)$
and
$M(H)$
and
 $M(H)^G$
is the image of
$M(H)^G$
is the image of
 $\operatorname {\mathrm {res}}$
.
$\operatorname {\mathrm {res}}$
.
The proof is the same as for the aforementioned theorem with a few very minor modifications, but it relies on the fact that
![]() $\vert H\vert $
and
$\vert H\vert $
and
![]() $\vert G : H\vert $
are relatively prime. Consequently, Proposition 3.1 does not hold in general for a Sylow
$\vert G : H\vert $
are relatively prime. Consequently, Proposition 3.1 does not hold in general for a Sylow
![]() $\pi $
-subgroup of G. However, the next result is an immediate consequence of Proposition 3.1(a).
$\pi $
-subgroup of G. However, the next result is an immediate consequence of Proposition 3.1(a).
Corollary 3.2. Suppose
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are Hall
$H_2$
are Hall
![]() $\pi $
-subgroups of
$\pi $
-subgroups of
![]() $G.$
Then
$G.$
Then
![]() $M(H_1)^G$
and
$M(H_1)^G$
and
![]() $M(H_2)^G$
are isomorphic.
$M(H_2)^G$
are isomorphic.
Despite this corollary, it is possible for two Hall
![]() $\pi $
-subgroups to possess nonisomorphic Schur multipliers as the following example illustrates.
$\pi $
-subgroups to possess nonisomorphic Schur multipliers as the following example illustrates.
Example 3.3. Using the nomenclature and results from [Reference Conway, Curtis, Norton, Parker and Wilson2], the Mathieu group
![]() $M_{23}$
has trivial Schur multiplier and has two conjugacy classes of Hall
$M_{23}$
has trivial Schur multiplier and has two conjugacy classes of Hall
![]() $\pi $
-subgroups for
$\pi $
-subgroups for
![]() $\pi = \{2, 3, 5, 7\}.$
Also, these Hall
$\pi = \{2, 3, 5, 7\}.$
Also, these Hall
![]() $\pi $
-subgroups are either isomorphic to
$\pi $
-subgroups are either isomorphic to
![]() $L_3(4):2_2$
or
$L_3(4):2_2$
or
![]() $2^4:A_7$
and the first of these groups has a cyclic Schur multiplier of order
$2^4:A_7$
and the first of these groups has a cyclic Schur multiplier of order
![]() $4,$
whereas for the second, it is cyclic of order
$4,$
whereas for the second, it is cyclic of order
![]() $6$
using Magma [Reference Bosma, Cannon and Playoust1].
$6$
using Magma [Reference Bosma, Cannon and Playoust1].
Given the close relationship between the Schur multiplier of a Hall
![]() $\pi $
-subgroup H of G and the Hall
$\pi $
-subgroup H of G and the Hall
![]() $\pi $
-subgroup of
$\pi $
-subgroup of
![]() $M(G)$
, one might expect a corresponding relationship between the
$M(G)$
, one might expect a corresponding relationship between the
![]() $\alpha _H$
-regular elements of H and the
$\alpha _H$
-regular elements of H and the
![]() $\alpha $
-regular
$\alpha $
-regular
![]() $\pi $
-elements of
$\pi $
-elements of
![]() $G.$
$G.$
Theorem 3.4. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $G.$
Let
$G.$
Let
![]() $x\in G$
and let
$x\in G$
and let
![]() $\pi $
be the set of prime numbers that divide
$\pi $
be the set of prime numbers that divide
![]() $o(x).$
For each
$o(x).$
For each
![]() $p_i\in \pi ,$
let
$p_i\in \pi ,$
let
![]() $P_i$
be a Sylow
$P_i$
be a Sylow
![]() $p_i$
-subgroup of
$p_i$
-subgroup of
![]() $C = C_G(x)$
and suppose that
$C = C_G(x)$
and suppose that
![]() $\alpha (g, x) = \alpha (x, g)$
for all
$\alpha (g, x) = \alpha (x, g)$
for all
![]() $g\in P_i.$
Then x is
$g\in P_i.$
Then x is
![]() $\alpha $
-regular in
$\alpha $
-regular in
![]() $G.$
$G.$
Proof. Using the assumption that
![]() $o(\alpha ) = o([\alpha ]), x$
is
$o(\alpha ) = o([\alpha ]), x$
is
![]() $\alpha $
-regular if and only if it is
$\alpha $
-regular if and only if it is
![]() $\alpha _{\pi }$
-regular and
$\alpha _{\pi }$
-regular and
![]() $\alpha _{\pi '}$
-regular. Now, x is
$\alpha _{\pi '}$
-regular. Now, x is
![]() $\alpha _{\pi '}$
-regular from Lemma 1.3, so we may assume
$\alpha _{\pi '}$
-regular from Lemma 1.3, so we may assume
![]() $\alpha = \alpha _{\pi }.$
Now,
$\alpha = \alpha _{\pi }.$
Now,
![]() $\alpha ': C\times \langle x\rangle \rightarrow \mathbb {C^*},$
defined by
$\alpha ': C\times \langle x\rangle \rightarrow \mathbb {C^*},$
defined by
![]() $\alpha '(g, x^i) = \alpha (g, x^i)/\alpha (x^i, g)$
for all
$\alpha '(g, x^i) = \alpha (g, x^i)/\alpha (x^i, g)$
for all
![]() $g\in C$
and all integers
$g\in C$
and all integers
![]() $i,$
is a pairing (see [Reference Karpilovsky4, Lemma 2.3.8]). The kernel K of the linear character
$i,$
is a pairing (see [Reference Karpilovsky4, Lemma 2.3.8]). The kernel K of the linear character
![]() $\alpha '(g, x)$
for all
$\alpha '(g, x)$
for all
![]() $g\in C$
has order divisible by
$g\in C$
has order divisible by
![]() $\vert P\vert $
for all Sylow p-subgroups P of
$\vert P\vert $
for all Sylow p-subgroups P of
![]() $C,$
by supposition for
$C,$
by supposition for
![]() $p\in \pi $
and by Lemma 1.3 otherwise. (Alternatively,
$p\in \pi $
and by Lemma 1.3 otherwise. (Alternatively,
![]() $\vert K\vert $
is divisible by
$\vert K\vert $
is divisible by
![]() $\vert P_i\vert $
for all
$\vert P_i\vert $
for all
![]() $p_i\in \pi $
by supposition and the group generated by the pairing
$p_i\in \pi $
by supposition and the group generated by the pairing
![]() $\alpha '$
is isomorphic to a subgroup of
$\alpha '$
is isomorphic to a subgroup of
![]() $C/K\otimes \langle x\rangle .$
This tensor product is trivial since the first group is a
$C/K\otimes \langle x\rangle .$
This tensor product is trivial since the first group is a
![]() $\pi '$
-group whereas the second is a
$\pi '$
-group whereas the second is a
![]() $\pi $
-group.)
$\pi $
-group.)
Two applications of Theorem 3.4 are recorded in the following corollaries.
Corollary 3.5. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G and let
$2$
-cocycle of G and let
![]() $x\in S$
be
$x\in S$
be
![]() $\alpha _S$
-regular for S, a Sylow
$\alpha _S$
-regular for S, a Sylow
![]() $\pi $
-subgroup of
$\pi $
-subgroup of
![]() $G.$
For each prime number
$G.$
For each prime number
![]() $p_i\in \pi ,$
let
$p_i\in \pi ,$
let
![]() $P_i$
be a Sylow
$P_i$
be a Sylow
![]() $p_i$
-subgroup of
$p_i$
-subgroup of
![]() $C_S(x)$
and suppose that
$C_S(x)$
and suppose that
![]() $P_i$
is a Sylow
$P_i$
is a Sylow
![]() $p_i$
-subgroup of
$p_i$
-subgroup of
![]() $C_G(x).$
Then x is
$C_G(x).$
Then x is
![]() $\alpha $
-regular in
$\alpha $
-regular in
![]() $G.$
$G.$
Proof. The set of prime numbers that divide
![]() $o(x)$
is a subset of
$o(x)$
is a subset of
![]() $\pi $
and so x is
$\pi $
and so x is
![]() $\alpha $
-regular in G from Theorem 3.4.
$\alpha $
-regular in G from Theorem 3.4.
Corollary 3.6. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G and let S be a Sylow
$2$
-cocycle of G and let S be a Sylow
![]() $\pi $
-subgroup of
$\pi $
-subgroup of
![]() $G.$
If S is normal in
$G.$
If S is normal in
![]() $G,$
then every
$G,$
then every
![]() $\alpha _S$
-regular element of S is
$\alpha _S$
-regular element of S is
![]() $\alpha $
-regular in
$\alpha $
-regular in
![]() $G.$
$G.$
Proof. Let
![]() $x\in S$
be
$x\in S$
be
![]() $\alpha _S$
-regular. Then
$\alpha _S$
-regular. Then
![]() $C_S(x) = C_G(x)\cap S$
is a normal Sylow
$C_S(x) = C_G(x)\cap S$
is a normal Sylow
![]() $\pi $
-subgroup of
$\pi $
-subgroup of
![]() $C_G(x)$
and Corollary 3.5 applies.
$C_G(x)$
and Corollary 3.5 applies.