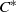Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T01:35:05.004Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPOID ${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM

Part of: Topological and differentiable algebraic systems General theory of linear operators Selfadjoint operator algebras

Published online by Cambridge University Press:  08 March 2013

GEOFF GOEHLE
GEOFF GOEHLE*
Affiliation:
Mathematics and Computer Science Department, Stillwell 426, Western Carolina University, Cullowhee, NC 28723, USA
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 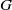$G$ is a second countable, locally compact Hausdorff groupoid with abelian stabiliser subgroups and a Haar system. We provide necessary and sufficient conditions for the groupoid 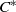${C}^{\ast } $-algebra to have Hausdorff spectrum. In particular, we show that the spectrum of 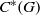${C}^{\ast } (G)$ is Hausdorff if and only if the stabilisers vary continuously with respect to the Fell topology, the orbit space 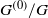${G}^{(0)} / G$ is Hausdorff, and, given convergent sequences 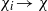${\chi }_{i} \rightarrow \chi $ and 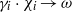${\gamma }_{i} \cdot {\chi }_{i} \rightarrow \omega $ in the dual stabiliser groupoid 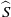$\widehat{S}$ where the 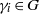${\gamma }_{i} \in G$ act via conjugation, if 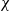$\chi $ and 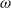$\omega $ are elements of the same fibre then 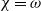$\chi = \omega $.

Keywords

groupoidC∗-algebrarepresentation theory

MSC classification

Secondary: 22A22: Topological groupoids (including differentiable and Lie groupoids) 47A67: Representation theory 46L99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 232 - 242
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Clark, L. O., ‘CCR and GCR groupoid ${C}^{\ast } $-algebras’, Indiana Univ. Math. J. 56 (5) (2007), 2087–2110.CrossRefGoogle Scholar
Goehle, G., ‘Group bundle duality’, Illinois J. Math. 52 (3) (2008), 951–956.CrossRefGoogle Scholar
Goehle, G., ‘The Mackey machine for regular groupoid crossed products. II’, Rocky Mountain J. Math. 42 (3) (2012), 1–28.CrossRefGoogle Scholar
Green, P., ‘${C}^{\ast } $-algebras of transformation groups with smooth orbit space’, Pacific J. Math. 72 (1) (1977), 71–97.CrossRefGoogle Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J., ‘Graphs, groupoids, and Cuntz–Krieger algebras’, J. Funct. Anal. 144 (1997), 505–541.CrossRefGoogle Scholar
Muhly, P. S., Renault, J. N. and Williams, D. P., ‘Equivalence and isomorphism for groupoid ${C}^{\ast } $-algebras’, J. Operator Theory 17 (1987), 3–22.Google Scholar
Muhly, P. S. and Williams, D. P., ‘Groupoid cohomology and the Dixmier–Douady class’, Proc. Lond. Math. Soc. 3 (1995), 109–134.CrossRefGoogle Scholar
Renault, J. N., Muhly, P. S. and Williams, D. P., ‘Continuous trace groupoid ${C}^{\ast } $-agebras, III’, Trans. Amer. Math. Soc. 348 (9) (1996), 3621–3641.Google Scholar
Pedersen, G., C ∗-algebras and their Automorphism Groups (Academic Press, London, 1979).Google Scholar
Raeburn, I., Graph Algebras, CBMS Regional Conference Series in Mathematics, 103 (American Mathematical Society, Providence, RI, 2005).CrossRefGoogle Scholar
Ramsay, A., ‘The Mackey–Glimm dichotomy for foliations and other Polish groupoids’, J. Funct. Anal. 94 (1990), 358–374.CrossRefGoogle Scholar
Renault, J., A Groupoid Approach to C ∗-algebras (Springer, Berlin, 1980).CrossRefGoogle Scholar
Renault, J., ‘The ideal structure of groupoid crossed product ${C}^{\ast } $-algebras’, J. Operator Theory 25 (1991), 3–36.Google Scholar
Williams, D. P., ‘Transformation group ${C}^{\ast } $-algebras with Hausdorff spectrum’, Illinois J. Math. 26 (2) (1982), 317–321.CrossRefGoogle Scholar