Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-25T23:32:34.133Z Has data issue: false hasContentIssue false
  • English
  • Français

GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER

Part of: Graph theory

Published online by Cambridge University Press:  13 September 2024

JIE CHEN Open the ORCID record for JIE CHEN [Opens in a new window]  and
SHOU-JUN XU Open the ORCID record for SHOU-JUN XU [Opens in a new window]
JIE CHEN
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China e-mail: [email protected]
SHOU-JUN XU*
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China and School of Mathematics and Statistics, Minnan Normal University, Zhangzhou, Fujian 363000, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In an isolate-free graph G, a subset S of vertices is a semitotal dominating set of G if it is a dominating set of G and every vertex in S is within distance 2 of another vertex of S. The semitotal domination number of G, denoted by 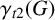$\gamma _{t2}(G)$, is the minimum cardinality of a semitotal dominating set in G. Goddard, Henning and McPillan [‘Semitotal domination in graphs’, Utilitas Math. 94 (2014), 67–81] characterised the trees and graphs of minimum degree 2 with semitotal domination number half their order. In this paper, we characterise all graphs whose semitotal domination number is half their order.

Keywords

dominationsemitotal domination

MSC classification

Primary: 05C69: Dominating sets, independent sets, cliques
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 2 , April 2025 , pp. 197 - 204
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was funded in part by National Natural Science Foundation of China (Grant No. 12071194) and the Chongqing Natural Science Foundation Innovation and Development Joint Fund (Municipal Education Commission) (Grant No. CSTB2022NSCQ-LZX0003).

References

Goddard, W., Henning, M. A. and McPillan, C. A., ‘Semitotal domination in graphs’, Util. Math. 94 (2014), 67–81.Google Scholar
Haynes, T. W., Hedetniemi, S. T. and Slater, P. J., Fundamentals of Domination in Graphs (CRC Press, Boca Raton, FL, 1998).Google Scholar
Haynes, T. W. and Henning, M. A., ‘Trees with unique minimum semitotal dominating sets’, Graphs Combin. 36 (2020), 689–702.CrossRefGoogle Scholar
Henning, M. A., ‘Edge weighting functions on semitotal dominating sets’, Graphs Combin. 33 (2017), 403–417.CrossRefGoogle Scholar
Henning, M. A., ‘Bounds on domination parameters in graphs: a brief survey’, Discuss. Math. Graph Theory 42 (2022), 665–708.CrossRefGoogle Scholar
Henning, M. A., Kang, L., Shan, E. and Yeo, A., ‘On matching and total domination in graphs’, Discrete Math. 308 (2008), 2313–2318.CrossRefGoogle Scholar
Henning, M. A. and Marcon, A. J., ‘On matching and semitotal domination in graphs’, Discrete Math. 324 (2014), 13–18.CrossRefGoogle Scholar
Henning, M. A. and Marcon, A. J., ‘Semitotal domination in claw-free cubic graphs’, Ann. Comb. 20(4) (2016), 1–15.CrossRefGoogle Scholar
Henning, M. A. and Pandey, A., ‘Algorithmic aspects of semitotal domination in graphs’, Theoret. Comput. Sci. 766 (2019), 46–57.CrossRefGoogle Scholar
Henning, M. A. and Yeo, A., Total Domination in Graphs (Springer, New York, 2013).CrossRefGoogle Scholar
Zhu, E. and Liu, C., ‘On the semitotal domination number of line graphs’, Discret. Appl. Math. 254 (2019), 295–298.CrossRefGoogle Scholar
Zhu, E., Shao, Z. and Xu, J., ‘Semitotal domination in claw-free cubic graphs’, Graphs Combin. 33 (2017), 1119–1130.CrossRefGoogle Scholar