No CrossRef data available.
Published online by Cambridge University Press: 30 January 2024
A group 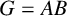 $G=AB$ is the weakly mutually permutable product of the subgroups A and B, if A permutes with every subgroup of B containing
$G=AB$ is the weakly mutually permutable product of the subgroups A and B, if A permutes with every subgroup of B containing 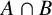 $A \cap B$ and B permutes with every subgroup of A containing
$A \cap B$ and B permutes with every subgroup of A containing 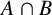 $A \cap B$. Weakly mutually permutable products were introduced by the first, second and fourth authors [‘Generalised mutually permutable products and saturated formations’, J. Algebra 595 (2022), 434–443] who showed that if
$A \cap B$. Weakly mutually permutable products were introduced by the first, second and fourth authors [‘Generalised mutually permutable products and saturated formations’, J. Algebra 595 (2022), 434–443] who showed that if 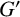 $G'$ is nilpotent, A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, then
$G'$ is nilpotent, A permutes with every Sylow subgroup of B and B permutes with every Sylow subgroup of A, then 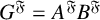 $G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}} $, where
$G^{\mathfrak {F}}=A^{\mathfrak {F}}B^{\mathfrak {F}} $, where 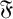 $ \mathfrak {F} $ is a saturated formation containing
$ \mathfrak {F} $ is a saturated formation containing 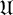 $ \mathfrak {U} $, the class of supersoluble groups. In this article we prove results on weakly mutually permutable products concerning
$ \mathfrak {U} $, the class of supersoluble groups. In this article we prove results on weakly mutually permutable products concerning 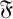 $ \mathfrak {F} $-residuals,
$ \mathfrak {F} $-residuals, 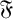 $ \mathfrak {F} $-projectors and
$ \mathfrak {F} $-projectors and 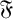 $\mathfrak {F}$-normalisers. As an application of some of our arguments, we unify some results on weakly mutually
$\mathfrak {F}$-normalisers. As an application of some of our arguments, we unify some results on weakly mutually 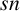 $sn$-products.
$sn$-products.
The work of the third author is supported by the Mathematical Center in Akademgorodok under agreement no. 075-15-2022-281 with the Ministry of Science and Higher Education of the Russian Federation.