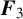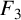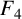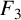Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Xiaoxia
and
Yu, Menglin
2023.
SOME NEW q-SUPERCONGRUENCES INVOLVING ONE FREE PARAMETER.
Rocky Mountain Journal of Mathematics,
Vol. 53,
Issue. 4,
He, Haihong
and
Wang, Xiaoxia
2023.
Some congruences that extend Van Hamme's (D.2) supercongruence.
Journal of Mathematical Analysis and Applications,
Vol. 527,
Issue. 1,
p.
127344.
He, Haihong
and
Wang, Xiaoxia
2024.
Two curious q-supercongruences and their extensions.
Forum Mathematicum,
Vol. 0,
Issue. 0,
Wang, Xiaoxia
and
Xu, Chang
2024.
q-supercongruences from Watson's 8φ7 transformation.
Forum Mathematicum,
WANG, XIAOXIA
and
YU, WENJIE
2025.
NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES
$F_1$
.
Bulletin of the Australian Mathematical Society,
Vol. 111,
Issue. 1,
p.
146.