Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Klavžar, Sandi
and
Yero, Ismael G.
2019.
The general position problem and strong resolving graphs.
Open Mathematics,
Vol. 17,
Issue. 1,
p.
1126.
Anand, Bijo S.
Chandran S. V., Ullas
Changat, Manoj
Klavžar, Sandi
and
Thomas, Elias John
2019.
Characterization of general position sets and its applications to cographs and bipartite graphs.
Applied Mathematics and Computation,
Vol. 359,
Issue. ,
p.
84.
Thomas, Elias John
and
Chandran S. V., Ullas
2020.
Characterization of classes of graphs with large general position number.
AKCE International Journal of Graphs and Combinatorics,
Vol. 17,
Issue. 3,
p.
935.
TIAN, JING
XU, KEXIANG
and
KLAVŽAR, SANDI
2021.
THE GENERAL POSITION NUMBER OF THE CARTESIAN PRODUCT OF TWO TREES.
Bulletin of the Australian Mathematical Society,
Vol. 104,
Issue. 1,
p.
1.
Klavžar, Sandi
Patkós, Balázs
Rus, Gregor
and
Yero, Ismael G.
2021.
On General Position Sets in Cartesian Products.
Results in Mathematics,
Vol. 76,
Issue. 3,
Klavžar, Sandi
Kuziak, Dorota
Peterin, Iztok
and
Yero, Ismael G.
2021.
A Steiner general position problem in graph theory.
Computational and Applied Mathematics,
Vol. 40,
Issue. 6,
Klavžar, Sandi
and
Rus, Gregor
2021.
The general position number of integer lattices.
Applied Mathematics and Computation,
Vol. 390,
Issue. ,
p.
125664.
Tian, Jing
and
Xu, Kexiang
2021.
The general position number of Cartesian products involving a factor with small diameter.
Applied Mathematics and Computation,
Vol. 403,
Issue. ,
p.
126206.
Zhang, Weidong
Yang, Xiaoping
and
Li, Juan
2022.
Sensor Placement for Leak Localization in Water Distribution Networks Based on Graph Convolutional Network.
IEEE Sensors Journal,
Vol. 22,
Issue. 21,
p.
21093.
Man, Jie
Dong, Honghui
Jia, Limin
and
Qin, Yong
2022.
AttGGCN Model: A Novel Multi-Sensor Fault Diagnosis Method for High-Speed Train Bogie.
IEEE Transactions on Intelligent Transportation Systems,
Vol. 23,
Issue. 10,
p.
19511.
Klavžar, Sandi
P.K., Neethu
and
S.V., Ullas Chandran
2022.
The general position achievement game played on graphs.
Discrete Applied Mathematics,
Vol. 317,
Issue. ,
p.
109.
Manuel, Paul
Prabha, R.
and
Klavžar, Sandi
2022.
The Edge General Position Problem.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 45,
Issue. 6,
p.
2997.
Di Stefano, Gabriele
2022.
Mutual visibility in graphs.
Applied Mathematics and Computation,
Vol. 419,
Issue. ,
p.
126850.
Tuite, James
Thomas, Elias John
and
Chandran S. V., Ullas
2022.
Algorithms and Discrete Applied Mathematics.
Vol. 13179,
Issue. ,
p.
36.
Kuziak, Dorota
and
Rodríguez-Velázquez, Juan A.
2023.
Total Mutual-Visibility in Graphs with Emphasis on Lexicographic and Cartesian Products.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 6,
Tian, Jing
Xu, Kexiang
and
Chao, Daikun
2023.
On the General Position Numbers of Maximal Outerplane Graphs.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 6,
Klavžar, Sandi
and
Tan, Elif
2023.
Edge General Position Sets in Fibonacci and Lucas Cubes.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 4,
Cicerone, Serafino
Di Stefano, Gabriele
and
Klavžar, Sandi
2023.
On the mutual visibility in Cartesian products and triangle-free graphs.
Applied Mathematics and Computation,
Vol. 438,
Issue. ,
p.
127619.
Korže, Danilo
and
Vesel, Aleksander
2023.
General Position Sets in Two Families of Cartesian Product Graphs.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 4,
KLAVŽAR, SANDI
KRISHNAKUMAR, ADITI
TUITE, JAMES
and
YERO, ISMAEL G.
2023.
TRAVERSING A GRAPH IN GENERAL POSITION.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 3,
p.
353.
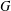 $G$, determine a largest set
$G$, determine a largest set 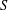 $S$ of vertices of
$S$ of vertices of 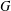 $G$ such that no three vertices of
$G$ such that no three vertices of 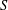 $S$ lie on a common geodesic. Such a set is a max-gp-set of
$S$ lie on a common geodesic. Such a set is a max-gp-set of 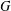 $G$ and its size is the gp-number
$G$ and its size is the gp-number 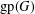 $\text{gp}(G)$ of
$\text{gp}(G)$ of 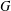 $G$. Upper bounds on
$G$. Upper bounds on 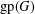 $\text{gp}(G)$ in terms of different isometric covers are given and used to determine the gp-number of several classes of graphs. Connections between general position sets and packings are investigated and used to give lower bounds on the gp-number. It is also proved that the general position problem is NP-complete.
$\text{gp}(G)$ in terms of different isometric covers are given and used to determine the gp-number of several classes of graphs. Connections between general position sets and packings are investigated and used to give lower bounds on the gp-number. It is also proved that the general position problem is NP-complete.