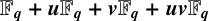 $\boldsymbol {\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q}$
$\boldsymbol {\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q}$Published online by Cambridge University Press: 15 December 2022
Wu and Shi [‘A note on k-Galois LCD codes over the ring
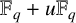 $\mathbb {F}_q + u\mathbb {F}_q$
’, Bull. Aust. Math. Soc. 104(1) (2021), 154–161] studied
$\mathbb {F}_q + u\mathbb {F}_q$
’, Bull. Aust. Math. Soc. 104(1) (2021), 154–161] studied
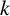 $ k $
-Galois LCD codes over the finite chain ring
$ k $
-Galois LCD codes over the finite chain ring
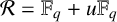 $\mathcal {R}=\mathbb {F}_q+u\mathbb {F}_q$
, where
$\mathcal {R}=\mathbb {F}_q+u\mathbb {F}_q$
, where
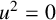 $u^2=0$
and
$u^2=0$
and
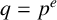 $ q=p^e$
for some prime p and positive integer e. We extend the results to the finite nonchain ring
$ q=p^e$
for some prime p and positive integer e. We extend the results to the finite nonchain ring
 $ \mathcal {R} =\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q$
, where
$ \mathcal {R} =\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q$
, where
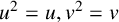 $u^2=u,v^2=v $
and
$u^2=u,v^2=v $
and
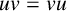 $ uv=vu $
. We define a correspondence between the
$ uv=vu $
. We define a correspondence between the
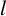 $ l $
-Galois dual of linear codes over
$ l $
-Galois dual of linear codes over
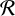 $ \mathcal {R} $
and the
$ \mathcal {R} $
and the
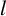 $ l $
-Galois dual of their component codes over
$ l $
-Galois dual of their component codes over
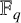 $ \mathbb {F}_q $
. Further, we construct Euclidean LCD and
$ \mathbb {F}_q $
. Further, we construct Euclidean LCD and
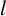 $ l $
-Galois LCD codes from linear codes over
$ l $
-Galois LCD codes from linear codes over
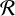 $ \mathcal {R} $
. We prove that any linear code over
$ \mathcal {R} $
. We prove that any linear code over
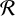 $ \mathcal {R} $
is equivalent to a Euclidean code over
$ \mathcal {R} $
is equivalent to a Euclidean code over
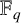 $\mathbb {F}_q$
with
$\mathbb {F}_q$
with
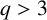 $ q>3 $
and an
$ q>3 $
and an
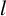 $ l $
-Galois LCD code over
$ l $
-Galois LCD code over
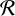 $ \mathcal {R}$
with
$ \mathcal {R}$
with
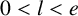 $0<l<e$
and
$0<l<e$
and
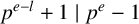 $p^{e-l}+1\mid p^e-1$
. Finally, we investigate MDS codes over
$p^{e-l}+1\mid p^e-1$
. Finally, we investigate MDS codes over
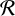 $ \mathcal {R}$
.
$ \mathcal {R}$
.
The first and second authors are supported by UGC, New Delhi, Govt. of India under grant DEC18-417932 and CSIR, New Delhi, Govt. of India under F. No. 09/086(1407)/2019-EMR-I, respectively.