Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T06:18:41.397Z Has data issue: false hasContentIssue false
  • English
  • Français

FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET

Part of: Ring extensions and related topics Chain conditions, finiteness conditions Complex dynamical systems Algebraic combinatorics Combinatorics Algebraic logic Finite commutative rings

Published online by Cambridge University Press:  20 February 2020

ALI JABALLAH Open the ORCID record for ALI JABALLAH [Opens in a new window]  and
NOÔMEN JARBOUI Open the ORCID record for NOÔMEN JARBOUI [Opens in a new window]
ALI JABALLAH
Affiliation:
Department of Mathematics, University of Sharjah, P.O. Box 27272, Sharjah, UAE email [email protected]
NOÔMEN JARBOUI*
Affiliation:
Department of Mathematics and Statistics, College of Science, King Faisal University, P.O. Box 400, Al-Ahsa31982, Saudi Arabia Département de Mathématiques, Faculté des Sciences de Sfax, Université de Sfax, Route de Soukra, P.O. Box 1171, Sfax3038, Tunisia email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 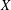$X$ be a nonempty set and 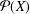${\mathcal{P}}(X)$ the power set of 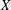$X$. The aim of this paper is to identify the unital subrings of 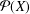${\mathcal{P}}(X)$ and to compute its cardinality when it is finite. It is proved that any topology $\unicode[STIX]{x1D70F}$ on 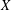$X$ such that 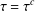$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}^{c}$, where 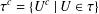$\unicode[STIX]{x1D70F}^{c}=\{U^{c}\mid U\in \unicode[STIX]{x1D70F}\}$, is a unital subring of 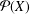${\mathcal{P}}(X)$. It is also shown that 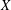$X$ is finite if and only if any unital subring of 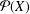${\mathcal{P}}(X)$ is a topology $\unicode[STIX]{x1D70F}$ on 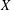$X$ such that 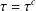$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}^{c}$ if and only if the set of unital subrings of 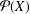${\mathcal{P}}(X)$ is finite. As a consequence, if 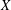$X$ is finite with cardinality 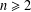$n\geq 2$, then the number of unital subrings of 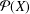${\mathcal{P}}(X)$ is equal to the $n$th Bell number and the supremum of the lengths of chains of unital subalgebras of 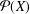${\mathcal{P}}(X)$ is equal to 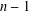$n-1$.

Keywords

integral extensionsubringintermediate ringBoolean algebrafinite topologypartitionBell numbers

MSC classification

Primary: 05E40: Combinatorial aspects of commutative algebra
Secondary: 03G05: Boolean algebras 05A18: Partitions of sets 06E05: Structure theory 06E10: Chain conditions, complete algebras 13B02: Extension theory 13B21: Integral dependence; going up, going down 13E99: None of the above, but in this section 13M05: Structure 13M99: None of the above, but in this section 37F20: Combinatorics and topology
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 15 - 20
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author thanks the University of Sharjah for funding Research Project No. 1902144081.

References

Ayache, A. and Jarboui, N., ‘Intermediary rings in normal pairs’, J. Pure Appl. Algebra 212(10) (2008), 2176–2181.10.1016/j.jpaa.2008.03.002CrossRefGoogle Scholar
Ben Nasr, M. and Jaballah, A., ‘Counting intermediate rings in normal pairs’, Expo. Math. 26 (2008), 163–175.10.1016/j.exmath.2007.09.002CrossRefGoogle Scholar
Ben Nasr, M. and Jaballah, A., ‘The number of intermediate rings in FIP extension of integral domains’, J. Algebra Appl. 19 (2020), Article ID 2050171, 12 pp.CrossRefGoogle Scholar
Benoumhani, M. and Jaballah, A., ‘Finite fuzzy topological spaces’, Fuzzy Sets and Systems 321 (2017), 101–114.CrossRefGoogle Scholar
Brinkmann, G. and McKay, B. D., ‘Counting unlabeled topologies and transitive relations’, J. Integer Seq. 8(2) (2005), Article ID 05.2.1, 7 pp.Google Scholar
Davis, D., ‘Overrings of commutative rings, II’, Trans. Amer. Math. Soc. 110 (1964), 196–212.CrossRefGoogle Scholar
Dobbs, D. E., Picavet, G. and Picavet-L’Hermitte, M., ‘Characterizing the ring extensions that satisfy FIP or FCP’, J. Algebra 371 (2012), 391–429.10.1016/j.jalgebra.2012.07.055CrossRefGoogle Scholar
Ferrand, D. and Olivier, J. P., ‘Homomorphismes minimaux d’anneaux’, J. Algebra 16 (1970), 461–471.10.1016/0021-8693(70)90020-7CrossRefGoogle Scholar
Gilmer, R., Multiplicative Ideal Theory (Dekker, New York, 1972).Google Scholar
Jaballah, A., ‘Subrings of ℚ’, J. Sci. Technol. 2(2) (1997), 1–13.Google Scholar
Jaballah, A., ‘A lower bound for the number of intermediary rings’, Comm. Algebra 27 (1999), 1307–1311.10.1080/00927879908826495CrossRefGoogle Scholar
Jaballah, A., ‘The number of overrings of an integrally closed domain’, Expo. Math. 23 (2005), 353–360.10.1016/j.exmath.2005.02.003CrossRefGoogle Scholar
Jaballah, A., ‘Ring extensions with some finiteness conditions on the set of intermediate rings’, Czechoslovak Math. J. 135(60) (2010), 117–124.10.1007/s10587-010-0002-xCrossRefGoogle Scholar
Jarboui, N. and Toumi, M. E., ‘Characterizing maximal non-Mori subrings of an integral domain’, Bull. Malays. Math. Sci. Soc. (2) 40(4) (2017), 1545–1557.CrossRefGoogle Scholar
Kaplansky, I., Commutative Rings (University of Chicago Press, Chicago, 1974).Google Scholar
Sharp, H. Jr., ‘Cardinality of finite topologies’, J. Combin. Theory 5 (1968), 82–86.CrossRefGoogle Scholar