Published online by Cambridge University Press: 17 April 2009
The question whether there exist non-free projective groups of rank r in the variety 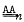 has been answered in the affirmative for n ≥ 2, r ≥ 2, except for n = r = 2, by V.A. Artamonov. This paper consists in a proof that a projective group G of rank 2 in
has been answered in the affirmative for n ≥ 2, r ≥ 2, except for n = r = 2, by V.A. Artamonov. This paper consists in a proof that a projective group G of rank 2 in 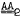 is free. If x and y are any two elements which generate G modulo
is free. If x and y are any two elements which generate G modulo 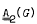 , then the group F generated by x and y is free in
, then the group F generated by x and y is free in 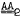 , and the index of F in G is finite and not divisible by 2. One wishes to replace x by xu and y by yν, where u and vν lie in
, and the index of F in G is finite and not divisible by 2. One wishes to replace x by xu and y by yν, where u and vν lie in 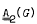 , so that 〈xu, yν〉 is the whole of G. This can be done: first, on general grounds, it is sufficient that 〈xu, yν〉 contain every C(a), where C(a) is the centralizer in the G/
, so that 〈xu, yν〉 is the whole of G. This can be done: first, on general grounds, it is sufficient that 〈xu, yν〉 contain every C(a), where C(a) is the centralizer in the G/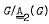 -module
-module 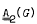 of an element a in
of an element a in 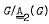 (and moreover choices of u and ν for each C(a) can be combined to give a single choice good for all C(a)); second, for the particular small numbers involved, the structure of C(a) is sufficiently simple for one to pick suitable u and ν without trouble.
(and moreover choices of u and ν for each C(a) can be combined to give a single choice good for all C(a)); second, for the particular small numbers involved, the structure of C(a) is sufficiently simple for one to pick suitable u and ν without trouble.