Hostname: page-component-599cfd5f84-jr95t Total loading time: 0 Render date: 2025-01-07T06:46:55.491Z Has data issue: false hasContentIssue false
  • English
  • Français

Free products of topological groups

Published online by Cambridge University Press:  17 April 2009

Sidney A. Morris
Sidney A. Morris
Affiliation:
University of Adelaide, Adelaide, South Australia, and University of Florida, Gainesville, Florida, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

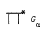In this note the notion of a free topological product Gα of a set {Gα} of topological groups is introduced. It is shown that it always exists, is unique and is algebraically isomorphic to the usual free product of the underlying groups. Further if each Gα is Hausdorff, then 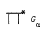Gα is Hausdorff and each Gα is a closed subgroup. Also 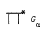Gα is a free topological group (respectively, maximally almost periodic) if each Gα is. This notion is then combined with the theory of varieties of topological groups developed by the author. For 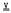a variety of topological groups, the 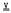-product of groups in 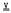is defined. It is shown that the 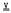-product,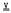 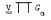Gα of any set {Gα} of groups in 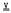exists, is unique and is algebraically isomorphic to the usual varietal product. It is noted that the 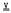-product of Hausdorff groups is not necessarily Hausdorff, but is if 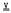is abelian. Each Gα is a quotient group of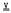 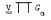Gα. It is proved that the 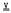-product of free topological groups of 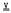and projective topological groups of 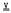are of the same type. Finally it is shown that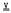 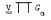Gα is connected if and only if each Gα is connected.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 4 , Issue 1 , February 1971 , pp. 17 - 29
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Dugundji, James, Topology (Allyn and Bacon, Boston, 1966).Google Scholar
[2]Golema, K., “Free products of compact general algebras”, Colloq. Math. 13 (1965), 165–166.CrossRefGoogle Scholar
[3]Graev, M.I., “Free topological groups”, Izv. Akad. Nauk SSSR Ser. Mat. 12 (1948), 279–324, (Russian). English transl., Amer. Math. Soc. Transl. no. 35, (1951). Reprint Amer. Math. Soc. Transl. (1) 8 (1962), 305–364.Google Scholar
[4]Hall, C.E., “Projective topological groups”, Proc. Amer. Math. Soc. 18 (1967), 425–431.CrossRefGoogle Scholar
[5]Hall, Marshall Jr, The theory of groups (The Macmillan Company, New York, 1959).Google Scholar
[6]Hewitt, Edwin and Ross, Kenneth A., Abstract harmonic analysis, Vol. I (Die Grundlehren der mathematischen Wissenschaften, Band 115; Springer-Verlag, Berlin, Göttingen, Heidelberg, 1963).Google Scholar
[7]Hulanicki, A., “Isomorphic embeddings of free products of compact groups”, Colloq. Math. 16 (1967), 235–241.CrossRefGoogle Scholar
[8]Kelley, John L., General topology (Van Nostrand, Toronto, New York, London, 1955).Google Scholar
[9]Markov, A.A., “On free topological groups”, C.R. (Doklady) Acad. Sci. URSS, (N.S.) 31 (1941), 299–301. Bull. Acad. Sci. URSS Sér. Math. [Izv. Adak. Nauk SSSR] 9 (1945), 3–64. (Russian. English summary). English Transl., Amer. Math. Soc. Transl. no. 30 (1950), 11–88; reprint Amer. Math. Soc. Transl. (1) 8 (1962), 195–272.Google Scholar
[10]Morris, Sidney A., “Varieties of topological groups”, Bull. Austral. Math. Soc. 1 (1969), 145–160.CrossRefGoogle Scholar
[11]Morris, Sidney A., “Varieties of topological groups II”, Bull. Austral. Math. Soc. 2 (1970), 1–13.CrossRefGoogle Scholar
[12]Morris, Sidney A., “Varieties of topological groups III”, Bull. Austral. Math. Soc. 2 (1970), 165–178.CrossRefGoogle Scholar
[13]Morris, Sidney A., “Varieties of topological groups”, Ph.D. thesis, The Flinders University of South Australia, February 1970. [Abstract: Bull. Austral. Math. Soc. 3 (1970), 429–431.]Google Scholar
[14]Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37, Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[15]Neumann, J. v., “Almost periodic functions in a group. I”, Trans. Amer. Math. Soc. 36 (1934), 445–492.CrossRefGoogle Scholar