Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T02:53:16.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Formal complexity of inverse semigroup rings

Published online by Cambridge University Press:  17 April 2009

Adel A. Shehadah
Adel A. Shehadah
Affiliation:
Mathematics Department, Yarmouk University, Irbid, Jordan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A ring (R, *) with involution * is called formally complex if 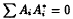implies that all Ai are 0. Let (R, *) be a formally complex ring and let S be an inverse semigroup. Let (R[S], *) be the semigroup ring with involution * defined by 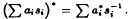. We show that (R[S], *) is a formally complex ring. Let (S, *) be a semigroup with proper involution *(aa* = ab* = bb* ⇒ a = b) and let (R, *′) be a formally complex ring. We give a sufficient condition for (R[S], *′) to be a formally complex ring and this condition is weaker than * being the inverse involution on S. We illustrate this by an example.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 41 , Issue 3 , June 1990 , pp. 343 - 346
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Drazin, M., ‘Regular Semigroups with Involution’, Symposium on Regular Semigroups, (Northern Illinois Univ. 1979), pp. 29–48.Google Scholar
[2]Shehadah, A., ‘Proper embeddability of Inverse Semigroups’, Bull. Austral. Math. Soc. 34 (1986), 383–387.CrossRefGoogle Scholar