Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T06:32:06.588Z Has data issue: false hasContentIssue false
  • English
  • Français

FIXED ELEMENTS OF NONINJECTIVE ENDOMORPHISMS OF POLYNOMIAL ALGEBRAS IN TWO VARIABLES

Part of: Rings and algebras with additional structure Ring extensions and related topics

Published online by Cambridge University Press:  20 October 2016

YUEYUE LI  and
JIE-TAI YU
YUEYUE LI*
Affiliation:
School of Mathematics, Jilin University, Changchun 130012, China email [email protected]
JIE-TAI YU
Affiliation:
College of Mathematics and Statistics, Shenzhen University, Shenzhen 518060, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 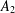$A_{2}$ be a free associative algebra or polynomial algebra of rank two over a field of characteristic zero. The main results of this paper are the classification of noninjective endomorphisms of 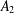$A_{2}$ and an algorithm to determine whether a given noninjective endomorphism of 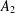$A_{2}$ has a nontrivial fixed element for a polynomial algebra. The algorithm for a free associative algebra of rank two is valid whenever an element is given and the subalgebra generated by this element contains the image of the given noninjective endomorphism.

Keywords

fixed elementfree associative algebrapolynomial algebraretract

MSC classification

Primary: 13B10: Morphisms
Secondary: 16W20: Automorphisms and endomorphisms
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 209 - 213
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The research of Yueyue Li was supported by NSF of China (Grant No. 11371165).

References

Bergman, G., ‘Centralizers in free associative algebras’, Trans. Amer. Math. Soc. 137 (1969), 327–344.Google Scholar
Drensky, V. and Yu, J.-T., ‘Retracts and test polynomials of polynomial algebras’, C. R. Acad. Bulgare Sci. 55(7) (2002), 11–14.Google Scholar
Drensky, V. and Yu, J.-T., ‘A cancellation conjecture for free associative algebras’, Proc. Amer. Math. Soc. 136 (2008), 3391–3394.CrossRefGoogle Scholar
von zur Gathen, J., ‘Functional decomposition of polynomials: the tame case’, J. Symbolic Comput. 9 (1990), 281–299.CrossRefGoogle Scholar
Gong, S.-J. and Yu, J.-T., ‘Test elements, retracts and automorphic orbits’, J. Algebra 320 (2008), 3062–3068.Google Scholar
Mikhalev, A. A., Shpilrain, V. and Yu, J.-T., Combinatorial Methods: Free Groups, Polynomials, and Free Algebras, CMS Books Mathematics, 19 (Springer, New York, 2004).Google Scholar
Mikhalev, A. A., Umirbaev, U. U. and Yu, J.-T., ‘Automorphic orbits in free non-associative algebras’, J. Algebra 243 (2001), 198–223.CrossRefGoogle Scholar
Mikhalev, A. A. and Yu, J.-T., ‘Test elements and retracts of free Lie algebras’, Comm. Algebra 25 (1997), 3283–3289.CrossRefGoogle Scholar
Mikhalev, A. A. and Yu, J.-T., ‘Test elements, retracts and automorphic orbits of free algebras’, Internat. J. Algebra Comput. 8 (1998), 295–310.Google Scholar
Mikhalev, A. A. and Zolotykh, A. A., ‘Test elements for monomorphisms of free Lie algebras and Lie superalgebras’, Comm. Algebra 23 (1995), 4995–5001.Google Scholar
Schinzel, A., Polynomials with Special Regard to Reducibility, Encyclopedia of Mathematics and its Applications, 77 (Cambridge University Press, Cambridge, 2000).CrossRefGoogle Scholar
Shestakov, I. P. and Umirbaev, U. U., ‘Poisson brackets and two-generated subalgebras of rings of polynomials’, J. Amer. Math. Soc. 17 (2004), 181–196.Google Scholar
Shpilrain, V. and Yu, J.-T., ‘Polynomial retracts and the Jacobian conjecture’, Trans. Amer. Math. Soc. 352 (2000), 477–484.Google Scholar
Turner, E., ‘Test words for automorphisms of free groups’, Bull. Lond. Math. Soc. 28 (1996), 255–263.Google Scholar