Article contents
The fit and flat components of barrelled spaces
Published online by Cambridge University Press: 17 April 2009
Abstract
The Splitting Theorem says that any given Hamel basis for a (Hausdorff) barrelled space E determines topologically complementary subspaces Ec and ED, and that Ec is flat, that is, contains no proper dense subspace. By use of this device it was shown that if E is non-flat it must contain a dense subspace of codimension at least ℵ0; here we maximally increase the estimate to ℵ1 under the assumption that the dominating cardinal ∂ equals ℵ1 [strictly weaker than the Continuum Hypothesis (CH)]. A related assumption strictly weaker than the Generalised CH allows us to prove that ED is fit, that is, contains a dense subspace whose codimension in ED is dim (ED), the largest imaginable. Thus the two components are extreme opposites, and E itself is fit if and only if dim (ED) ≥ dim (Ec), in which case there is a choice of basis for which ED = E. Morover, E is non-flat (if and) only if the codimension of E′ is at least 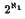 in E*. These results ensure latitude in the search for certain subspaces of E* transverse to E′, as in the barrelled countable enlargement (BCE) problem, and show that every non-flat GM-space has a BCE.
in E*. These results ensure latitude in the search for certain subspaces of E* transverse to E′, as in the barrelled countable enlargement (BCE) problem, and show that every non-flat GM-space has a BCE.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1995
References
- 14
- Cited by


