Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T02:36:33.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Hilbert transforms and compactness

Published online by Cambridge University Press:  17 April 2009

Susumu Okada
Susumu Okada
Affiliation:
Department of Mathematics, University of Tasmania, GPO Box 252C Hobart Tas 7001
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that for the finite Hilbert transform Tp on the Banach space Lp(]–1, 1[), 1 < p < ∞, the linear operator 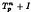is not strictly singular whenever n is a positive integer.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 46 , Issue 3 , December 1992 , pp. 475 - 478
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Gohberg, I. and Krupnik, N., Einführung in die Theorie des eindimensional singulären Integraloperatoren, (German translation) (Birkhäuser Verlag, Basel, Boston, Stuttgart, 1979).CrossRefGoogle Scholar
[2]Jörgens, K., Linear integral operators, (English translation) (Pitman, Boston, London, Melbourne, 1982).Google Scholar
[3]Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I (Springer-Verlag, Berlin, Heidelberg, New York, 1977).CrossRefGoogle Scholar
[4]Mikhlin, S.G. and Prössdorf, S., Singular integral operators, (English translation) (Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1986).CrossRefGoogle Scholar
[5]Okada, S. and Elliott, D., ‘The finite Hilbert transform in L2’, Math. Nachr. 153 (1991), 43–56.CrossRefGoogle Scholar
[6]Riesz, M., ‘Sur les fonctions conjuguées’, Math. Z. 27 (1927), 218–244.CrossRefGoogle Scholar
[7]Söhngen, H., ‘Zur Theorie der endlichen Hilbert-Transformation’, Math. Z. 60 (1954), 31–51.CrossRefGoogle Scholar