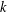Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T11:00:20.361Z Has data issue: false hasContentIssue false
  • English
  • Français

FACTORS OF CARMICHAEL NUMBERS AND AN EVEN WEAKER $k$-TUPLES CONJECTURE

Part of: Elementary number theory

Published online by Cambridge University Press:  20 February 2019

THOMAS WRIGHT
THOMAS WRIGHT*
Affiliation:
429 N. Church St., Spartanburg, SC 29302, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the open questions in the study of Carmichael numbers is whether, for a given 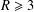$R\geq 3$, there exist infinitely many Carmichael numbers with exactly 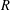$R$ prime factors. Chernick [‘On Fermat’s simple theorem’, Bull. Amer. Math. Soc.45 (1935), 269–274] proved that Dickson’s 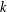$k$-tuple conjecture would imply a positive result for all such 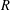$R$. Wright [‘Factors of Carmichael numbers and a weak 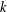$k$-tuples conjecture’, J. Aust. Math. Soc.100(3) (2016), 421–429] showed that a weakened version of Dickson’s conjecture would imply that there are an infinitude of 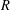$R$ for which there are infinitely many such Carmichael numbers. In this paper, we improve on our 2016 result by weakening the required conjecture even further.

Keywords

Carmichael numberGranville–Pomerance conjectureDickson’s k-tuple conjecture

MSC classification

Primary: 11A51: Factorization; primality
Secondary: 11A41: Primes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 376 - 384
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Alford, W. R., Granville, A. and Pomerance, C., ‘There are infinitely many Carmichael numbers’, Ann. of Math. (2) 139(3) (1994), 703–722.10.2307/2118576Google Scholar
Baker, R. C. and Schmidt, W. M., ‘Diophantine problems in variables restricted to the values 0 and 1’, J. Number Theory 12(4) (1980), 460–486.10.1016/0022-314X(80)90039-6Google Scholar
Chernick, J., ‘On Fermat’s simple theorem’, Bull. Amer. Math. Soc. (N.S.) 45 (1935), 269–274.10.1090/S0002-9904-1939-06953-XGoogle Scholar
Carmichael, R. D., ‘Note on a new number theory function’, Bull. Amer. Math. Soc. (N.S.) 16 (1910), 232–238.10.1090/S0002-9904-1910-01892-9Google Scholar
Van Emde Boas, P. and Kruyswijk, D., ‘A combinatorial problem on finite Abelian groups’, in: Afdeling Zuivere Wisk, Vol. 3 (Math. Centrum, Amsterdam, 1969).Google Scholar
Erdős, P., ‘On pseudoprimes and Carmichael numbers’, Publ. Math. Debrecen 4 (1956), 201–206.Google Scholar
Granville, A. and Pomerance, C., ‘Two contradictory conjectures concerning Carmichael numbers’, Math. Comp. 71 (2002), 883–908.10.1090/S0025-5718-01-01355-2Google Scholar
Korselt, A., ‘Problème chinois’, L’intermédinaire des mathématiciens 6 (1899), 142–143.Google Scholar
Maynard, J., ‘Small gaps between primes’, Ann. of Math. (2) 181 (2015), 383–413.10.4007/annals.2015.181.1.7Google Scholar
Meshulam, R., ‘An uncertainty inequality and zero subsums’, Discrete Math. 84(2) (1990), 197–200.10.1016/0012-365X(90)90375-RGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., ‘The large sieve’, Mathematika 20 (1973), 119–134.10.1112/S0025579300004708Google Scholar
Rosser, J. B. and Schoenfeld, L., ‘Approximate formulas for some functions of prime numbers’, Illinois J. Math. 6 (1962), 64–94.10.1215/ijm/1255631807Google Scholar
Wright, T., ‘Factors of Carmichael numbers and a weak k-tuples conjecture’, J. Aust. Math. Soc. 100(3) (2016), 421–429.10.1017/S1446788715000427Google Scholar
Wright, T., ‘There are infinitely many elliptic Carmichael numbers’, Bull. London Math. Soc. 50(5) (2018), 791–800.10.1112/blms.12185Google Scholar