No CrossRef data available.
Article contents
FACTORING VARIANTS OF CHEBYSHEV POLYNOMIALS WITH MINIMAL POLYNOMIALS OF 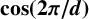 $\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
$\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
Published online by Cambridge University Press: 21 March 2022
Abstract
We solve the problem of factoring polynomials
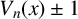 $V_n(x) \pm 1$
and
$V_n(x) \pm 1$
and
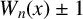 $W_n(x) \pm 1$
, where
$W_n(x) \pm 1$
, where
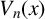 $V_n(x)$
and
$V_n(x)$
and
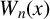 $W_n(x)$
are Chebyshev polynomials of the third and fourth kinds, in terms of the minimal polynomials of
$W_n(x)$
are Chebyshev polynomials of the third and fourth kinds, in terms of the minimal polynomials of
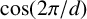 $\cos ({2\pi }{/d})$
. The method of proof is based on earlier work, D. A. Wolfram, [‘Factoring variants of Chebyshev polynomials of the first and second kinds with minimal polynomials of
$\cos ({2\pi }{/d})$
. The method of proof is based on earlier work, D. A. Wolfram, [‘Factoring variants of Chebyshev polynomials of the first and second kinds with minimal polynomials of
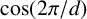 $\cos ({2 \pi }/{d})$
’, Amer. Math. Monthly 129 (2022), 172–176] for factoring variants of Chebyshev polynomials of the first and second kinds. We extend this to show that, in general, similar variants of Chebyshev polynomials of the fifth and sixth kinds,
$\cos ({2 \pi }/{d})$
’, Amer. Math. Monthly 129 (2022), 172–176] for factoring variants of Chebyshev polynomials of the first and second kinds. We extend this to show that, in general, similar variants of Chebyshev polynomials of the fifth and sixth kinds,
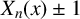 $X_n(x) \pm 1$
and
$X_n(x) \pm 1$
and
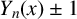 $Y_n(x) \pm 1$
, do not have factors that are minimal polynomials of
$Y_n(x) \pm 1$
, do not have factors that are minimal polynomials of
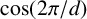 $\cos ({2\pi }/{d})$
.
$\cos ({2\pi }/{d})$
.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 448 - 457
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.



