No CrossRef data available.
Published online by Cambridge University Press: 08 April 2020
Barnard and Steinerberger [‘Three convolution inequalities on the real line with connections to additive combinatorics’, Preprint, 2019, arXiv:1903.08731] established the autocorrelation inequality 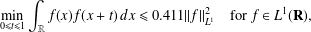 $$\begin{eqnarray}\min _{0\leq t\leq 1}\int _{\mathbb{R}}f(x)f(x+t)\,dx\leq 0.411||f||_{L^{1}}^{2}\quad \text{for}~f\in L^{1}(\mathbf{R}),\end{eqnarray}$$
$$\begin{eqnarray}\min _{0\leq t\leq 1}\int _{\mathbb{R}}f(x)f(x+t)\,dx\leq 0.411||f||_{L^{1}}^{2}\quad \text{for}~f\in L^{1}(\mathbf{R}),\end{eqnarray}$$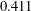 $0.411$ cannot be replaced by
$0.411$ cannot be replaced by 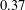 $0.37$. In addition to being interesting and important in their own right, inequalities such as these have applications in additive combinatorics. We show that for
$0.37$. In addition to being interesting and important in their own right, inequalities such as these have applications in additive combinatorics. We show that for 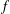 $f$ to be extremal for this inequality, we must have
$f$ to be extremal for this inequality, we must have 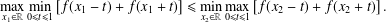 $$\begin{eqnarray}\max _{x_{1}\in \mathbb{R}}\min _{0\leq t\leq 1}\left[f(x_{1}-t)+f(x_{1}+t)\right]\leq \min _{x_{2}\in \mathbb{R}}\max _{0\leq t\leq 1}\left[f(x_{2}-t)+f(x_{2}+t)\right].\end{eqnarray}$$
$$\begin{eqnarray}\max _{x_{1}\in \mathbb{R}}\min _{0\leq t\leq 1}\left[f(x_{1}-t)+f(x_{1}+t)\right]\leq \min _{x_{2}\in \mathbb{R}}\max _{0\leq t\leq 1}\left[f(x_{2}-t)+f(x_{2}+t)\right].\end{eqnarray}$$ $f$ to increase the value of the autocorrelation, while leaving
$f$ to increase the value of the autocorrelation, while leaving  $||f||_{L^{1}}$ unchanged. These perturbation methods can be extended to examine a more general notion of autocorrelation. Let
$||f||_{L^{1}}$ unchanged. These perturbation methods can be extended to examine a more general notion of autocorrelation. Let  $d,n\in \mathbb{Z}^{+}$,
$d,n\in \mathbb{Z}^{+}$, 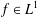 $f\in L^{1}$,
$f\in L^{1}$, 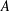 $A$ be a
$A$ be a 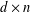 $d\times n$ matrix with real entries and columns
$d\times n$ matrix with real entries and columns 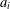 $a_{i}$ for
$a_{i}$ for 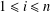 $1\leq i\leq n$ and
$1\leq i\leq n$ and 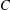 $C$ be a constant. For a broad class of matrices
$C$ be a constant. For a broad class of matrices 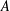 $A$, we prove necessary conditions for
$A$, we prove necessary conditions for 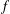 $f$ to extremise autocorrelation inequalities of the form
$f$ to extremise autocorrelation inequalities of the form 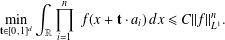 $$\begin{eqnarray}\min _{\mathbf{t}\in [0,1]^{d}}\int _{\mathbb{R}}\mathop{\prod }_{i=1}^{n}~f(x+\mathbf{t}\cdot a_{i})\,dx\leq C||f||_{L^{1}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\min _{\mathbf{t}\in [0,1]^{d}}\int _{\mathbb{R}}\mathop{\prod }_{i=1}^{n}~f(x+\mathbf{t}\cdot a_{i})\,dx\leq C||f||_{L^{1}}^{n}.\end{eqnarray}$$
This work was supported by NSF grants DMS1659037 and DMS1561945, Wake Forest University and Williams College.