Article contents
EXTENDING RESULTS OF MORGAN AND PARKER ABOUT COMMUTING GRAPHS
Published online by Cambridge University Press: 11 May 2021
Abstract
Morgan and Parker proved that if G is a group with
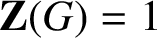 ${\textbf{Z}(G)} = 1$
, then the connected components of the commuting graph of G have diameter at most
${\textbf{Z}(G)} = 1$
, then the connected components of the commuting graph of G have diameter at most
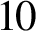 $10$
. Parker proved that if, in addition, G is solvable, then the commuting graph of G is disconnected if and only if G is a Frobenius group or a
$10$
. Parker proved that if, in addition, G is solvable, then the commuting graph of G is disconnected if and only if G is a Frobenius group or a
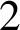 $2$
-Frobenius group, and if the commuting graph of G is connected, then its diameter is at most
$2$
-Frobenius group, and if the commuting graph of G is connected, then its diameter is at most
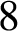 $8$
. We prove that the hypothesis
$8$
. We prove that the hypothesis
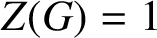 $Z (G) = 1$
in these results can be replaced with
$Z (G) = 1$
in these results can be replaced with
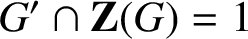 $G' \cap {\textbf{Z}(G)} = 1$
. We also prove that if G is solvable and
$G' \cap {\textbf{Z}(G)} = 1$
. We also prove that if G is solvable and
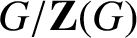 $G/{\textbf{Z}(G)}$
is either a Frobenius group or a
$G/{\textbf{Z}(G)}$
is either a Frobenius group or a
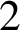 $2$
-Frobenius group, then the commuting graph of G is disconnected.
$2$
-Frobenius group, then the commuting graph of G is disconnected.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 92 - 100
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by NSF Grant DMS-1653002.
References
- 3
- Cited by



