No CrossRef data available.
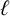 $\ell $-REGULAR NONOVERLINED PARTS
$\ell $-REGULAR NONOVERLINED PARTSPublished online by Cambridge University Press: 25 November 2024
Recently, Alanazi et al. [‘Refining overpartitions by properties of nonoverlined parts’, Contrib. Discrete Math. 17(2) (2022), 96–111] considered overpartitions wherein the nonoverlined parts must be 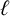 $\ell $-regular, that is, the nonoverlined parts cannot be divisible by the integer
$\ell $-regular, that is, the nonoverlined parts cannot be divisible by the integer 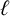 $\ell $. In the process, they proved a general parity result for the corresponding enumerating functions. They also proved some specific congruences for the case
$\ell $. In the process, they proved a general parity result for the corresponding enumerating functions. They also proved some specific congruences for the case 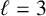 $\ell =3$. In this paper we use elementary generating function manipulations to significantly extend this set of known congruences for these functions.
$\ell =3$. In this paper we use elementary generating function manipulations to significantly extend this set of known congruences for these functions.